
【题目】已知:如图,在△ABC中,D、E分别是AB、BC边上的中点,过点C作CF∥AB,交DE的延长线于F点,连接CD、BF.
(1)求证:△BDE≌△CFE;
(2)△ABC满足什么条件时,四边形BDCF是矩形?

【答案】(1)详见解析;(2)当BC=AC时,四边形BDCF是矩形,理由详见解析
【解析】
(1)由平行线的性质得出∠DBE=∠CFE,由中点的定义得出BE=CE,由ASA证明△BDE≌△CFE即可;
(2)先证明DE是△ABC的中位线,得出DE∥AC,证出四边形BDCF是平行四边形,得出AD=CF,证出CF=BD,得出四边形BDCF是平行四边形;再由等腰三角形的性质得出CD⊥AB,即可得出结论.
(1)证明:∵CF∥AB,
∴∠DBE=∠CFE,
∵E是BC的中点,
∴BE=CE,
在△BDE和△CFE中,
∴△BDE≌△CFE(ASA);
(2)解:当BC=AC时,四边形BDCF是矩形,理由如下:
∵D、E分别是AB,BC的中点
∴DE是△ABC的中位线,
∴DE∥AC,又AF∥BC,
∴四边形BDCF是平行四边形,
∴AD=CF,
又BD=AD,
∴CF=BD,又CF∥BD,
∴四边形BDCF是平行四边形;
∵BC=AC,BD=AD,
∴CD⊥AB,即∠BDC=90°,
∴平行四边形BDCF是矩形.



 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】阅读理解:
如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.
解决问题:
(1)如图1,∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB和BC的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF.
(1)求证:△AEH≌△CGF;
(2)若EG平分∠HEF,求证:四边形EFGH是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某研究性学习小组进行了探究活动.如图,已知一架竹梯AB斜靠在墙角MON处,竹梯AB=13m,梯子底端离墙角的距离BO=5m.
(1)求这个梯子顶端A距地面有多高;
(2)如果梯子的顶端A下滑4 m到点C,那么梯子的底部B在水平方向上滑动的距离BD=4 m吗?为什么?
(3)亮亮在活动中发现无论梯子怎么滑动,在滑动的过程中梯子上总有一个定点到墙角O的距离始终是不变的定值,会思考问题的你能说出这个点并说明其中的道理吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11分)如图,抛物线y=ax2+bx﹣3与x轴交于A,B两点,与y轴交于C点,且经过点(2,﹣3a),对称轴是直线x=1,顶点是M.
(1)求抛物线对应的函数表达式;
(2)经过C,M两点作直线与x轴交于点N,在抛物线上是否存在这样的点P,使以点P,A,C,N为顶点的四边形为平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)设直线y=﹣x+3与y轴的交点是D,在线段BD上任取一点E(不与B,D重合),经过A,B,E三点的圆交直线BC于点F,试判断△AEF的形状,并说明理由;
(4)当E是直线y=﹣x+3上任意一点时,(3)中的结论是否成立(请直接写出结论).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张长为7cm,宽为5cm的矩形纸片上,现在剪下一个腰长为4cm的等腰三角形,要求等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上,则剪下的等腰三角形一腰上的的高为_____________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )

A. 15 B. 18 C. 21 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
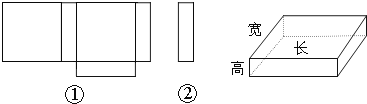
(1)小明总共剪开了 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在图上补 全.(请在备用图中画出所有可能)
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的4倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是720cm,求这个长方体纸盒的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空并解答:
规定:a2=a×a,a3=a×a×a,an=a×a×…×a(n 个 a)
(1)(2×3)2= ,22×32= ,你发现(2× 3)2 的值与 22×32 的值 .
(2)(2×3)3= ,23×33= ,你发现(2×3)3 的值与 23×33 的值 .
由此,我们可以猜想:(a×b)2 a2×b2,(a×b)3 a3×b3,…(a×b)n an×bn.
(3)利用(2)题结论计算(﹣2)2018×(﹣![]() )2019 的值.
)2019 的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com