
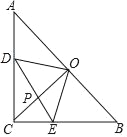
【题目】在Rr△ABC中,∠C=90°,AC=BC=1,点O为AB的中点,点D、E分别为AC、AB边上的动点,且保持DO⊥EO,连接CO、DE交于点P.
(1)求证:OD=OE;
(2)在运动的过程中,DPEP是否存在最大值?若存在,请求出DPEP的最大值;若不存在,请说明理由.
(3)若CD=2CE,求DP的长度.
【答案】(1)证明见解析(2)DPEP存在最大值为![]() (3)PG=
(3)PG=![]() ,PD=
,PD=![]()
【解析】
(1)证明△ADO≌△CEO,可得OD=OE;
(2)先根据对角互补证明D、C、E、O四点共圆,再得△DPO∽△CPE,列比例式可得:PDEP=CPPO,设CP=x,则OP=![]() ﹣x,则CPPO=x(
﹣x,则CPPO=x(![]() ﹣x )=﹣
﹣x )=﹣![]() ,根据二次函数的最值问题得出DPEP存在最大值为
,根据二次函数的最值问题得出DPEP存在最大值为![]() ;
;
(3)设CE=a,则CD=2a,根据AC=1列等式求出,a=![]() ,则CE=
,则CE=![]() ,CD=
,CD=![]() ,根据勾股定理求DE的长,作辅助线构建平行线,得相似,列比例式可求得DP的长.
,根据勾股定理求DE的长,作辅助线构建平行线,得相似,列比例式可求得DP的长.
证明:(1)∵AC=BC=1,点O为AB的中点,
∴CO⊥AB,CO=AO,
∴∠COA=90°,
∴∠DOP+∠AOD=90°,
∵DO⊥OE,
∴∠DOP+∠POE=90°,
∴∠AOD=∠POE,
同理∠A=∠OCE,
∴△ADO≌△CEO,
∴OD=OE;
(2)∵∠ACB=90°,∠DOE=90°,
∴∠ACB+∠DOE=180°,
∴D、C、E、O四点共圆,
∴∠ODP=∠PCE,∠DPO=∠CPE,
∴△DPO∽△CPE,
∴![]() ,
,
∴PDEP=CPPO,
在Rt△ACB中,AB=![]() ,
,
∴CO=AO=BO=![]() ,
,
设CP=x,则OP=![]() ﹣x,
﹣x,
则CPPO=x(![]() ﹣x )=﹣
﹣x )=﹣![]() =﹣(x﹣
=﹣(x﹣![]() )2+
)2+![]() ,
,
即当x=![]() 时,CPPO有最大值为
时,CPPO有最大值为![]() ,
,
也就是DPEP存在最大值为![]() ;
;
(3)设CE=a,则CD=2a,
由(1)得:AD=CE=a,
∵AC=1,
∴a+2a=1,
a=![]() ,
,
∴CE=![]() ,CD=
,CD=![]() ,
,
由勾股定理得:DE=![]() ,
,
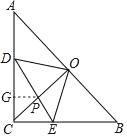
过P作PG∥BC,交AC于G,
∵∠DCO=45°,
∴PG=CG,
∵PG∥CE,
∴△DGP∽△DCE,
∴![]() ,
,
∴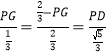 ,
,
∴PG=![]() ,PD=
,PD=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连接CD,EB.
(1)图中还有几对全等三角形,请你一一列举;
(2)求证:CF=EF.

查看答案和解析>>
科目:初中数学 来源: 题型:
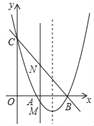
【题目】如图,抛物线y=x2+bx+c与x轴交于点A和B(3,0),与y轴交于点C(0,3).
(1)求抛物线的解析式;
(2)若点M是抛物线上在x轴下方的动点,过M作MN∥y轴交直线BC于点N,求线段MN的最大值;
(3)E是抛物线对称轴上一点,F是抛物线上一点,是否存在以A,B,E,F为顶点的四边形是平行四边形?若存在,请直接写出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
第1个等式:![]()
第2个等式:![]()
第3等式:![]()
第4个等式:![]()
请解答下列问题:
(1)按以上规律写出第5个等式:a5= = .
(2)用含n的式子表示第n个等式:an= = (n为正整数).
(3)求a1+a2+a3+a4+…+a2018的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
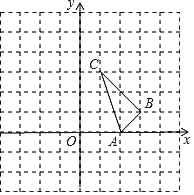
【题目】如图,在平面直角坐标系中,已知A(2,0)、B(3,1)、C(1,3).
(1)将△ABC沿x轴负方向移动2个单位长度至△A1B1C1,画图并写出点C1的坐标;
(2)以点A1为旋转中心,将△A1B1C1逆时针方向旋转90°得到△A2B2C2,画图并写出点C2的坐标;
(3)以B、C1、C2为顶点的三角形是 三角形,其外接圆的半径R= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B为定点,定直线l//AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:
①线段MN的长;
②△PAB的周长;
③△PMN的面积;
④直线MN,AB之间的距离;
⑤∠APB的大小.
其中会随点P的移动而变化的是( )

A. ②③ B. ②⑤ C. ①③④ D. ④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于58元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售粽子多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=﹣2x+100.(利润=售价﹣制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月能获得350万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
(3)根据相关部门规定,这种电子产品的销售单价不能高于32元,如果厂商要获得每月不低于350万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com