
【题目】某电子厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=﹣2x+100.(利润=售价﹣制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月能获得350万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
(3)根据相关部门规定,这种电子产品的销售单价不能高于32元,如果厂商要获得每月不低于350万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?
【答案】(1)z=﹣2x2+136x﹣1800;(2)25元或43元;当销售单价为34元时,每月能获得最大利润,最大利润是512万元;(3)648万元.
【解析】
(1)根据每月的利润z=(x﹣18)y,再把y=﹣2x+100代入即可求出z与x之间的函数解析式,
(2)把z=350代入z=﹣2x2+136x﹣1800,解这个方程即可,把函数关系式变形为顶点式运用二次函数的性质求出最值;
(3)根据销售单价不能高于32元,厂商要获得每月不低于350万元的利润得出销售单价的取值范围,进而解决问题.
(1)z=(x﹣18)y=(x﹣18)(﹣2x+100)=﹣2x2+136x﹣1800,
∴z与x之间的函数解析式为z=﹣2x2+136x﹣1800;
(2)由z=350,得350=﹣2x2+136x﹣1800,
解这个方程得x1=25,x2=43,
所以,销售单价定为25元或43元,
将z═﹣2x2+136x﹣1800配方,得z=﹣2(x﹣34)2+512,
因此,当销售单价为34元时,每月能获得最大利润,最大利润是512万元;
(3)结合(2)及函数z=﹣2x2+136x﹣1800的图象(如图所示)可知,
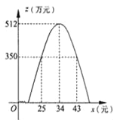
当25≤x≤43时z≥350,
又由限价32元,得25≤x≤32,
根据一次函数的性质,得y=﹣2x+100中y随x的增大而减小,
∴当x=32时,每月制造成本最低.最低成本是18×(﹣2×32+100)=648(万元),
因此,所求每月最低制造成本为648万元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
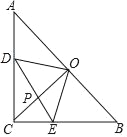
【题目】在Rr△ABC中,∠C=90°,AC=BC=1,点O为AB的中点,点D、E分别为AC、AB边上的动点,且保持DO⊥EO,连接CO、DE交于点P.
(1)求证:OD=OE;
(2)在运动的过程中,DPEP是否存在最大值?若存在,请求出DPEP的最大值;若不存在,请说明理由.
(3)若CD=2CE,求DP的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了“打造川东北教育高地,办区域内最好教育”,我市部分学校开展英语小班教学,某校对“英语小班教学”的喜爱情况进行了随机凋查.对收集的信息进行统计,绘制了下面两副尚不完整的统计图.请你根据统计图所提供的信息解答下列问题:图中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”.
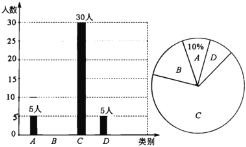
(1)被调查的总人数是____人,扇形统计图中C部分所对应的扇形圆心角的度数为_______;
(2)补全条形统计图;
(3)若该校共有学生2800人,请根据上述调查结果,估计该校学生中A类有______人;
(4)在抽取的A类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树形图或列表法求出被抽到的两个学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC的边长是2,以BC边上的高AB1为边作等边三角形,得到第一个等边△AB1C1;再以等边△AB1C1的B1C1边上的高AB2为边作等边三角形,得到第二个等边△AB2C2;再以等边△AB2C2的B2C2边上的高AB3为边作等边三角形,得到第三个等边△AB3C3;…,记△B1CB2的面积为S1,△B2C1B3的面积为S2,△B3C2B4的面积为S3,如此下去,则Sn=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数解析式为y=2x2﹣4x﹣6.
(1)写出抛物线的开口方向,顶点M坐标,对称轴,最值;
(2)求抛物线与x轴交点A,B与y轴的交点C的坐标;
(3)作出函数的图象;
(4)观察图象:x为何值时,y随x的增大而增大;
(5)观察图象:当x何值时,y>0;当x何值时,y=0;当x何值时,y<0.
查看答案和解析>>
科目:初中数学 来源: 题型:
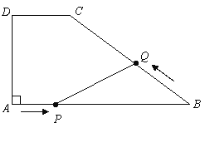
【题目】如图,在梯形ABCD中,DC//AB,∠A=90°,AD=6cm,DC=4cm,BC的坡度i=3:4,动点P从A出发以2cm/s的速度沿AB方向向点B运动,动点Q从点B出发以3厘cm/s的速度沿B→C→D方向向点D运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止.设动点运动的时间为t秒.
(1)求边BC的长;
(2)当t为何值时,PC与BQ相互平分;
(3)连结PQ,设△PBQ的面积为y,探求y与t的函数关系式,求t为何值时,y有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一天,水果经营户老张用1600元从水果批发市场批发猕猴桃和芒果共50千克,后再到水果市场去卖,已知猕猴桃和芒果当天的批发价和零售价如表所示:
品名 | 猕猴桃 | 芒果 |
批发价 | 20 | 40 |
零售价 | 26 | 50 |
![]() 他购进的猕猴桃和芒果各多少千克?
他购进的猕猴桃和芒果各多少千克?
![]() 如果猕猴桃和芒果全部卖完,他能赚多少钱?
如果猕猴桃和芒果全部卖完,他能赚多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
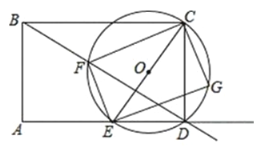
【题目】如图,矩形![]() 的边
的边![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 移动,以
移动,以![]() 为直径作圆
为直径作圆![]() ,点
,点![]() 为圆
为圆![]() 与射线
与射线![]() 的公共点,连接
的公共点,连接![]() ,过点
,过点![]() 作
作![]() ,
,![]() 与圆
与圆![]() 相交于点
相交于点![]() , 连接
, 连接![]() .
.
(1)试说明四边形![]() 是矩形;
是矩形;
(2)当圆![]() 与射线
与射线![]() 相切时,点
相切时,点![]() 停止移动,在点
停止移动,在点![]() 移动的过程中:
移动的过程中:
①矩形![]() 的面积是否存在最大值或最小值?若存在,求出这个最大值或最小值;若不存在,说明理由;
的面积是否存在最大值或最小值?若存在,求出这个最大值或最小值;若不存在,说明理由;
②求点![]() 移动路线的长.
移动路线的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】密码锁有三个转轮,每个转轮上有十个数字:0,1,2,…9.小黄同学是9月份中旬出生,用生日“月份+日期”设置密码:9××(注:中旬为某月中的11日﹣20日),小张同学要破解其密码:
(1)第一个转轮设置的数字是9,第二个转轮设置的数字可能是 .
(2)请你帮小张同学列举出所有可能的密码,并求密码数能被3整除的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com