
【题目】已知二次函数解析式为y=2x2﹣4x﹣6.
(1)写出抛物线的开口方向,顶点M坐标,对称轴,最值;
(2)求抛物线与x轴交点A,B与y轴的交点C的坐标;
(3)作出函数的图象;
(4)观察图象:x为何值时,y随x的增大而增大;
(5)观察图象:当x何值时,y>0;当x何值时,y=0;当x何值时,y<0.
【答案】(1)抛物线的开口向上,![]() ;
;![]() ;
;![]() .(2)A(﹣1,0),B(3,0),(0,﹣6);(3)见解析;(4)当x>1时y随x的增大而增大;(5)当x<﹣1或x>3时,y>0;当x=﹣1或x=3时y=0;当﹣1<x<3时y<0.
.(2)A(﹣1,0),B(3,0),(0,﹣6);(3)见解析;(4)当x>1时y随x的增大而增大;(5)当x<﹣1或x>3时,y>0;当x=﹣1或x=3时y=0;当﹣1<x<3时y<0.
【解析】
(1)将函数解析式化为顶点式即可解答本题;
(2)根据函数解析式可以求得与x轴和y轴的交点,本题得以解决;
(3)根据(1)、(2)中求得的点的坐标可以画出相应的函数图象;
(4)根据图象可以解答本题;
(5)根据图象可以解答本题.
(1)∵二次函数解析式为y=2x2﹣4x﹣6=2(x﹣1)2﹣8,
∴抛物线的开口向上,顶点M的坐标为(1,﹣8),对称轴是直线x=1,最小值是y=﹣8;
(2)∵二次函数解析式为y=2x2﹣4x﹣6,
∴当x=0时,y=﹣6,当y=0时,x1=3,x2=﹣1,
∴点A的坐标为(﹣1,0),点B的坐标为(3,0),点C的坐标为(0,﹣6);
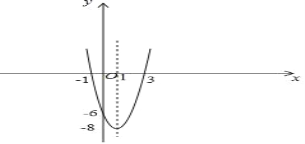
(3)函数图象如右图所示;
(4)由图象可知,当x>1时y随x的增大而增大;
(5)由图象可知,当x<﹣1或x>3时,y>0;
当x=﹣1或x=3时y=0;
当﹣1<x<3时y<0.


科目:初中数学 来源: 题型:
【题目】观察下列等式:
第1个等式:![]()
第2个等式:![]()
第3等式:![]()
第4个等式:![]()
请解答下列问题:
(1)按以上规律写出第5个等式:a5= = .
(2)用含n的式子表示第n个等式:an= = (n为正整数).
(3)求a1+a2+a3+a4+…+a2018的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从热气球C上测得两建筑物A、B底部的俯角分别为30°和60度.如果这时气球的高度CD为90米.且点A、D、B在同一直线上,求建筑物A、B间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者.在消防车上点A处测得点B和点C的仰角分别是45°和65°,点A距地面2.5米,点B距地面10.5米.为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,![]() ≈1.4)
≈1.4)

查看答案和解析>>
科目:初中数学 来源: 题型:
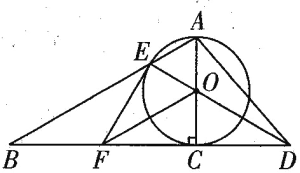
【题目】如图,以RtABC的直角边AC为直径作O交斜边AB于点E,连接EO并延长交BC的延长线于点D,作OF//AB交BC于点F,连接EF、EC.
(1)求证:OFCE;
(2)求证:EF是O的切线;
(3)若O的半径为3,EAC60,求tanADE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=﹣2x+100.(利润=售价﹣制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月能获得350万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
(3)根据相关部门规定,这种电子产品的销售单价不能高于32元,如果厂商要获得每月不低于350万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=(x-2)2+m与x轴交于点A和B,与y轴交于点C,点D是点C关于抛物线对称轴的对称点,若点A的坐标为(1,0),直线y2=kx+b经过点A,D.
(1)求抛物线的函数解析式;
(2)求点D的坐标和直线AD的函数解析式;
(3)根据图象指出,当x取何值时,y2>y1.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 ![]() 轴于点
轴于点 ![]() ,点
,点![]() 是直线
是直线 ![]() 上的动点.直线
上的动点.直线 ![]() 交
交 ![]() 于点
于点 ![]() ,过点
,过点 ![]() 作直线
作直线 ![]() 垂直于
垂直于 ![]() ,垂足为
,垂足为 ![]() ,过点
,过点 ![]() ,
,![]() 的直线
的直线 ![]() 交
交 ![]() 于点 E,当直线
于点 E,当直线 ![]() ,
,![]() ,
,![]() 能围成三角形时,设该三角形面积为
能围成三角形时,设该三角形面积为 ![]() ,当直线
,当直线 ![]() ,
,![]() ,
,![]() 能围成三角形时,设该三角形面积为
能围成三角形时,设该三角形面积为 ![]() .
.
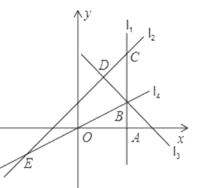
(1)若点 ![]() 在线段
在线段 ![]() 上,且
上,且 ![]() ,则
,则 ![]() 点坐标为_________;
点坐标为_________;
(2)若点 ![]() 在直线
在直线![]() 上,且
上,且![]() ,则
,则![]() 的度数为_______.
的度数为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
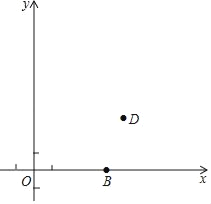
【题目】在平面直角坐标系![]() 中(如图),已知抛物线
中(如图),已知抛物线![]() 的图象经过点
的图象经过点![]() 、
、![]() ,设它与
,设它与![]() 轴的另一个交点为
轴的另一个交点为![]() (点
(点![]() 在点
在点![]() 的左侧),且
的左侧),且![]() 的面积是3.
的面积是3.
(1)求该抛物线的表达式;
(2)求![]() 的正切值;
的正切值;
(3)若抛物线与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 在射线
在射线![]() 上,当
上,当![]() 与
与![]() 相似时,求点
相似时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com