
【题目】如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连接CD,EB.
(1)图中还有几对全等三角形,请你一一列举;
(2)求证:CF=EF.

【答案】(1) △ADC≌△ABE,△CDF≌△EBF;(2)证明见解析.
【解析】试题分析:(1)根据Rt△ABC≌Rt△ADE,得出AC=AE,BC=DE,AB=AD,∠ACB=∠AED,∠BAC=∠DAE,从而推出∠CAD=∠EAB,△ACD≌△AEB,△CDF≌△EBF;
(2)先证得△CDF≌△EBF,进而得到CF=EF.
试题解析:(1)图中其它的全等三角形为:△ACD≌△AEB,△DCF≌△BEF;
(2)∵Rt△ABC≌Rt△ADE,
∴AC=AE,AD=AB,∠CAB=∠EAD,
∴∠CAB-∠DAB=∠EAD-∠DAB.
即∠CAD=∠EAB.
∴△CAD≌△EAB,
∴CD=EB,∠ADC=∠ABE.
又∵∠ADE=∠ABC,
∴∠CDF=∠EBF.
又∵∠DFC=∠BFE,
∴△CDF≌△EBF.
∴CF=EF.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料:
如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2=![]() 交于A(1,3)和B(﹣3,﹣1)两点.
交于A(1,3)和B(﹣3,﹣1)两点.
观察图象可知:
①当x=﹣3或1时,y1=y2;
②当﹣3<x<0或x>1时,y1>y2,即通过观察函数的图象,可以得到不等式ax+b>![]() 的解集.
的解集.
有这样一个问题:求不等式x3+4x2﹣x﹣4>0的解集.
某同学根据学习以上知识的经验,对求不等式x3+4x2﹣x﹣4>0的解集进行了探究.

下面是他的探究过程,请将(2)、(3)、(4)补充完整:
(1)将不等式按条件进行转化:
当x=0时,原不等式不成立;
当x>0时,原不等式可以转化为x2+4x﹣1>![]() ;
;
当x<0时,原不等式可以转化为x2+4x﹣1<![]() ;
;
(2)构造函数,画出图象
设y3=x2+4x﹣1,y4=![]() ,在同一坐标系中分别画出这两个函数的图象.
,在同一坐标系中分别画出这两个函数的图象.
双曲线y4=![]() 如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
(3)确定两个函数图象公共点的横坐标
观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为 ;
(4)借助图象,写出解集
结合(1)的讨论结果,观察两个函数的图象可知:不等式x3+4x2﹣x﹣4>0的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
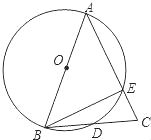
【题目】已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°.
(1)求∠EBC的度数;
(2)求证:BD=CD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com