
分析 ①正确.由c≠0,a+b=ab=c,推出ab≠0,推出$\frac{a+b}{ab}$=1,即$\frac{1}{a}$+$\frac{1}{b}$=1,故正确.
②错误.由a=3,a+b=ab=c,推出3+b=3b=c,推出b=$\frac{3}{2}$,c=$\frac{9}{2}$,推出b+c=$\frac{3}{2}$+$\frac{9}{2}$=6,故②错误.
③正确.分三种情形讨论即可.
解答 解:∵c≠0,a+b=ab=c,
∴ab≠0,
∴$\frac{a+b}{ab}$=1,
∴$\frac{1}{a}$+$\frac{1}{b}$=1,故①正确.
∵a=3,a+b=ab=c,
∴3+b=3b=c,
∴b=$\frac{3}{2}$,c=$\frac{9}{2}$,
∴b+c=$\frac{3}{2}$+$\frac{9}{2}$=6,故②错误,
∵a、b、c中只有两个数相等,
假设a=b,则有2a=a2=c,
∴a=2或0(舍弃),
∴a=b=2,c=4,
∴a+b+c=8,
假设a=c,则有b+c=bc=c,则a=b=c=0,不合题意,同理b=c也不合题意,故③正确,
故答案为①③.
点评 本题考查分式的加减、等式的性质、一元一次方程等知识,解题的关键是理解题意,学会用分类讨论的思想思考问题,属于中考常考题型.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我市重庆路水果市场某水果店购进甲、乙两种水果.已知1千克甲种水果的进价比1千克乙种水果的进价多4元,购进2千克甲种水果与1千克乙种水果共需20元.
我市重庆路水果市场某水果店购进甲、乙两种水果.已知1千克甲种水果的进价比1千克乙种水果的进价多4元,购进2千克甲种水果与1千克乙种水果共需20元.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
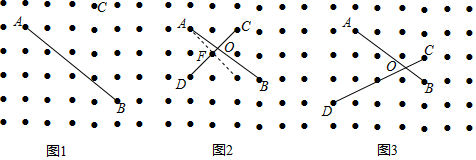
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com