
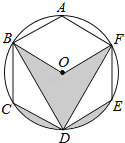
【题目】如图,正六边形ABCDEF内接于⊙O,若⊙O的半径为4,则阴影部分的面积等于 .
【答案】![]() π.
π.
【解析】
试题分析:先正确作辅助线,构造扇形和等边三角形、直角三角形,分别求出两个弓形的面积和两个三角形面积,即可求出阴影部分的面积.
解:连接OC、OD、OE,OC交BD于M,OE交DF于N,过O作OZ⊥CD于Z,
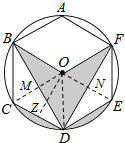
∵六边形ABCDEF是正六边形,
∴BC=CD=DE=EF,∠BOC=∠COD=∠DOE=∠EOF=60°,
由垂径定理得:OC⊥BD,OE⊥DF,BM=DM,FN=DN,
∵在Rt△BMO中,OB=4,∠BOM=60°,
∴BM=OB×sin60°=2![]() ,OM=OBcos60°=2,
,OM=OBcos60°=2,
∴BD=2BM=4![]() ,
,
∴△BDO的面积是![]() ×BD×OM=
×BD×OM=![]() ×4
×4![]() ×2=4
×2=4![]() ,
,
同理△FDO的面积是4![]() ;
;
∵∠COD=60°,OC=OD=4,
∴△COD是等边三角形,
∴∠OCD=∠ODC=60°,
在Rt△CZO中,OC=4,OZ=OC×sin60°=2![]() ,
,
∴S扇形OCD﹣S△COD=![]() ﹣
﹣![]() ×4×2
×4×2![]() =
=![]() π﹣4
π﹣4![]() ,
,
∴阴影部分的面积是:4![]() +4
+4![]() +
+![]() π﹣4
π﹣4![]() +
+![]() π﹣4
π﹣4![]() =
=![]() π,
π,
故答案为:π.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】2011年长江中下游地区发生了特大旱情.为抗旱保丰收,某地政府制定了农户投资购买抗旱设备的补贴办法,其中购买Ⅰ型、Ⅱ型抗旱设备投资的金额与政府补的额度存在下表所示的函数对应关系.

(1)分别求y1和y2的函数解析式;
(2)有一农户同时对Ⅰ型、Ⅱ型两种设备共投资10万元购买,请你设计一个能获得最大补贴金额的方案,并求出按此方案能获得的最大补贴金额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张正面分别标有数字:﹣1,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
(1)请用列表或画树形图的方法(只选其中一种),表示两次抽出卡片上的数字的所有结果;
(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点(x,y)落在双曲线上y=![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(﹣1,0).有下列结论:
①abc>0;
②4a﹣2b+c<0;
③4a+b=0;
④抛物线与x轴的另一个交点是(5,0);
⑤点(﹣3,y1),(6,y2)都在抛物线上,则有y1<y2.
其中正确的是( )
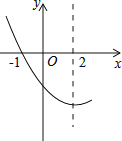
A.①②③ B.②④⑤ C.①③④ D.③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=﹣x2+2mx﹣m2+1的对称轴是直线x=1.
(1)求抛物线的表达式;
(2)点D(n,y1),E(3,y2)在抛物线上,若y1<y2,请直接写出n的取值范围;
(3)设点M(p,q)为抛物线上的一个动点,当﹣1<p<2时,点M关于y轴的对称点都在直线y=kx﹣4的上方,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com