
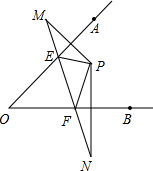
 如图,点P在∠AOB的内部,点M,N分别是点P关于直线OA,OB的对称点,线段MN交OA,OB于点E,F.
如图,点P在∠AOB的内部,点M,N分别是点P关于直线OA,OB的对称点,线段MN交OA,OB于点E,F.分析 (1)根据轴对称的性质得出ME=PE,NF=PF,再由△PEF的周长是15cm即可得出结论;
(2)要求∠EPF的度数,要在△EPF中进行,根据轴对称的性质和等腰三角形的性质找出与∠MPN的关系,利用已知∠AOB=35°可求出∠EPF,答案可得.
解答 解:(1)∵点M、N分别是点P关于OA、OB的对称点,
∴ME=PE,NF=PF,△PEF的周长是15cm,
∴ME+EF+NF=PE+EF+PF=MN=15cm,
即MN=15cm.
(2)如图,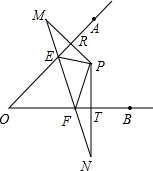
∵点M、N分别是点P关于直线0A、OB的对称点,
∴OA垂直平分PM,OB垂直平分PN,
∴ME=PE,PF=NF,
∴∠PEF=2∠M,∠PFE=2∠N,
∵∠PRE=∠PTF=90°,
∴在四边形OTPR中,
∴∠MPN+∠AOB=180°,
∵∠EPF+2∠M+2∠N=180°,
即∠MPN+∠M+∠N=180°,
∴∠M+∠N=∠AOB=35°
∴∠EPF=180°-35°×2=110°.
点评 本题主要考查了轴对称的性质、线段垂直平分线的性质,在计算的过程中运用了四边形的内角和和三角形的内角和定理及其推论.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:解答题
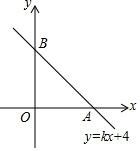 如图,在直角坐标系中,直线y=kx+4与x轴正半轴交于一点A,与y轴交于点B,已知△OAB的面积为10,求
如图,在直角坐标系中,直线y=kx+4与x轴正半轴交于一点A,与y轴交于点B,已知△OAB的面积为10,求查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
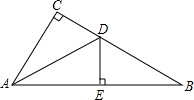 如图,在直角△ABC中,∠C=90°,∠CAB的平分线AD交BC于点D,若DE垂直平分AB.
如图,在直角△ABC中,∠C=90°,∠CAB的平分线AD交BC于点D,若DE垂直平分AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 品名 | 黄瓜 | 茄子 |
| 批发价/(元/千克) | 2.4 | 2.2 |
| 零售价/(元/千克) | 3.6 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
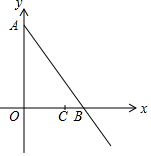 如图:在平面直角坐标系中,点O为坐标原点,△AOB的面积为18$\sqrt{3}$,∠ABO=60°,点C在OB上,OC=4,BC=2,动点P从A点出发沿射线AB以每秒2个单位的速度运动,连接OP.
如图:在平面直角坐标系中,点O为坐标原点,△AOB的面积为18$\sqrt{3}$,∠ABO=60°,点C在OB上,OC=4,BC=2,动点P从A点出发沿射线AB以每秒2个单位的速度运动,连接OP.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
| 100 | 150 | -400 | 350 | -100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com