
【题目】问题背景:已知在△ABC中,边AB上的动点D由A向B运动(与A,B不重合),同时点E由点C沿BC的延长线方向运动(E不与C重合),连接DE交AC于点F,点H是线段AF上一点,求 ![]() 的值.
的值.
(1)初步尝试
如图(1),若△ABC是等边三角形,DH⊥AC,且点D、E的运动速度相等,小王同学发现可以过点D作DG∥BC交AC于点G,先证GH=AH,再证GF=CF,
从而求得 ![]() 的值为 .
的值为 . 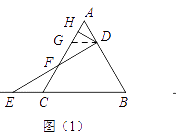
(2)类比探究
如图(2),若△ABC中,∠ABC=90°,∠ADH=∠BAC=30°,且点D,E的运动速度之比是 ![]() :1,求
:1,求 ![]() 的值.
的值.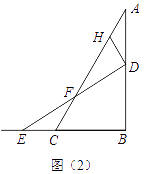
(3)延伸拓展
如图(3)若在△ABC中,AB=AC,∠ADH=∠BAC=36°,记 ![]() =m,且点D、E的运动速度相等,试用含m的代数式表示
=m,且点D、E的运动速度相等,试用含m的代数式表示 ![]() 的值(直接写出果,不必写解答过程).
的值(直接写出果,不必写解答过程).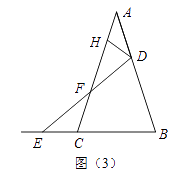
【答案】
(1)2
(2)
解:如图(2)过点D作DG∥BC交AC于点G,
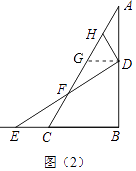
则∠ADG=∠ABC=90°.
∵∠BAC=∠ADH=30°,
∴AH=DH,∠GHD=∠BAC+∠ADH=60°,
∠HDG=∠ADG﹣∠ADH=60°,
∴△DGH为等边三角形.
∴GD=GH=DH=AH,AD=GDtan60°= ![]() GD.
GD.
由题意可知,AD= ![]() CE.
CE.
∴GD=CE.
∵DG∥BC,
∴∠GDF=∠CEF.
在△GDF与△CEF中, 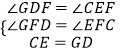 ,
,
∴△GDF≌△CEF(AAS),
∴GF=CF.
GH+GF=AH+CF,即HF=AH+CF,
∴HF= ![]() AC=2,即
AC=2,即 ![]() .
.
(3)
解: ![]() =
= ![]() .理由如下:
.理由如下:
如图(3),过点D作DG∥BC交AC于点G,
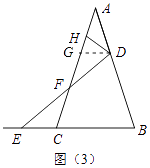
易得AD=AG,AD=EC,∠AGD=∠ACB.
在△ABC中,∵∠BAC=∠ADH=36°,AB=AC,
∴AH=DH,∠ACB=∠B=72°,∠GHD=∠HAD+∠ADH=72°.
∴∠AGD=∠GHD=72°.
∵∠GHD=∠B=∠HGD=∠ACB,
∴△ABC∽△DGH.
∴ ![]() ,
,
∴GH=mD H=mA H.
由△ADG∽△ABC可得 ![]() .
.
∵DG∥BC,
∴ ![]() .
.
∴FG=mFC.
∴GH+FG=m(AH+FC)=m(AC﹣HF),
即HF=m(AC﹣HF).
∴ ![]() =
= ![]() .
.
【解析】解:(1)过点D作DG∥BC交AC于点G,如图(1)所示:
∵△ABC是等边三角形,
∴△AGD是等边三角形,
∴AD=GD,
由题意知:CE=AD,
∴CE=GD
∵DG∥BC,
∴∠GDF=∠CEF,
在△GDF与△CEF中, 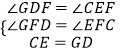 ,
,
∴△GDF≌△CEF(AAS),
∴CF=GF,
∵DH⊥AG,
∴AH=GH,
∴AC=AG+CG=2GH+2GF=2(GH+GF),
HF=GH+GF,
∴ ![]() =2;
=2;
故答案为:2;
(1)过点D作DG∥BC交AC于点G,由题意知△AGD是等边三角形,所以AD=GD,所以可以证明△GDF≌△CEF,所以CF=GF,由三线合一可知:AH=GH,即可得出所求答案;(2)过点D作DG∥BC交AC于点G,由点D,E的运动速度之比是 ![]() :1可知GD=CE,所以可以证明△GDF≌△CEF,所以CF=GF,由∠ABC=90°,∠ADH=∠BAC=30°可知:AH=DH,即可得出答案;(3)类似(1)(2)的方法可求出
:1可知GD=CE,所以可以证明△GDF≌△CEF,所以CF=GF,由∠ABC=90°,∠ADH=∠BAC=30°可知:AH=DH,即可得出答案;(3)类似(1)(2)的方法可求出 ![]() =m和
=m和 ![]() =m,然后利用GH+FG=m(AH+FC)=m(AC﹣HF)即可求出
=m,然后利用GH+FG=m(AH+FC)=m(AC﹣HF)即可求出 ![]() 的值.
的值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】王老师的数学课采用小组合作学习的方式,把班上40名学生分成若干个小组.如果要求每小组只能是5人或6人,那么分组方案有( )
A. 4种 B. 3种 C. 2种 D. 1种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接DE并延长至点F,使EF=DE,连接AF、DC.求证:四边形ADCF是菱形. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE.将△EDC绕点C按顺时针方向旋转,当△EDC旋转到A,D,E三点共线时,线段BD的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度,他们在A处测得信号塔顶端P的仰角是45°,信号塔底端点Q的仰角为31°,沿水平地面向前走100米到B处,测得信号塔顶端P的仰角是68°,求信号塔PQ的高度.(结果精确到0.1米,参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.48,tan31°≈0.60,sin31°≈0.52,cos31°≈0.86)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解决线段数量关系问题中,如果条件中有角平分线,经常采用下面构造全等三角形的解决思路.如:在图1中,若![]() 是
是![]() 的平分线
的平分线![]() 上一点,点
上一点,点![]() 在
在![]() 上,此时,在
上,此时,在![]() 截取
截取![]() ,连接
,连接![]() ,根据三角形全等的判定
,根据三角形全等的判定![]() ,容易构造出全等三角形⊿
,容易构造出全等三角形⊿![]() 和⊿
和⊿![]() ,参考上面的方法,解答下列问题:
,参考上面的方法,解答下列问题:

如图2,在非等边⊿![]() 中,
中, ![]() ,
, ![]() 分别是
分别是![]() 的平分线,且
的平分线,且![]() 交于点
交于点![]() .求证:
.求证: ![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
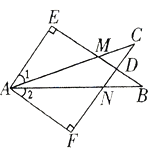
【题目】如图,在△ABE和△ACF中,EB交AC于点M,交FC于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF.下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中,正确的是_________.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把两条中线互相垂直的三角形称为“中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均为“中垂三角形”,设BC=a,AC=b,AB=c.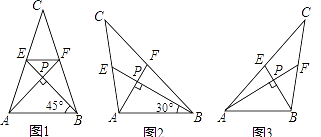
(1)【特例探索】
如图1,当∠ABE=45°,c=2 ![]() 时,a= , b=;如图2,当∠ABE=30°,c=4时,a= , b=;
时,a= , b=;如图2,当∠ABE=30°,c=4时,a= , b=;
(2)【归纳证明】
请你观察(1)中的计算结果,猜想a2 , b2 , c2三者之间的关系,用等式表示出来,请利用图3证明你发现的关系式;
(3)【拓展应用】
如图4,在ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=2 ![]() ,AB=3.求AF的长.
,AB=3.求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 与x轴的负半轴交于点A,与y轴交于点B,连结AB.点C
与x轴的负半轴交于点A,与y轴交于点B,连结AB.点C ![]() 在抛物线上,直线AC与y轴交于点D.
在抛物线上,直线AC与y轴交于点D.
(1)求c的值及直线AC的函数表达式;
(2)点P在x轴的正半轴上,点Q在y轴正半轴上,连结PQ与直线AC交于点M,连结MO并延长交AB于点N,若M为PQ的中点.
①求证:△APM∽△AON;
②设点M的横坐标为m , 求AN的长(用含m的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com