
【题目】如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度,他们在A处测得信号塔顶端P的仰角是45°,信号塔底端点Q的仰角为31°,沿水平地面向前走100米到B处,测得信号塔顶端P的仰角是68°,求信号塔PQ的高度.(结果精确到0.1米,参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.48,tan31°≈0.60,sin31°≈0.52,cos31°≈0.86)
【答案】解:延长PQ交直线AB于点M,连接AQ,如图所示: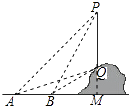
则∠PMA=90°,
设PM的长为x米,
在Rt△PAM中,∠PAM=45°,
∴AM=PM=x米,
∴BM=x﹣100(米),
在Rt△PBM中,∵tan∠PBM= ![]() ,
,
∴tan68°= ![]() ≈2.48,
≈2.48,
解得:x≈167.57,
在Rt△QAM中,∵tan∠QAM= ![]() ,
,
∴QM=AMtan∠QAM=167.57×tan31°≈167.57×0.60≈100.54(米),
∴PQ=PM﹣QM=167.57﹣100.54≈67.0(米);信号塔PQ的高度约为67.0米.
【解析】延长PQ交直线AB于点E,连接AQ,设PM的长为x米,先由三角函数得出方程求出PM,再由三角函数求出QM,得出PQ的长度即可.
【考点精析】通过灵活运用关于坡度坡角问题,掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA即可以解答此题.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平整的地面上,用若干个棱长完全相同的小正方体堆成一个几何体.
(1)请画出这个几何体的三视图.
(2)如果现在你手头还有一些相同的小正方体,要求保持俯视图和左视图不变,最多可以再添加几个小正方体


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张直角三角形纸片BEC的斜边放在矩形ABCD的BC边上,恰好完全重合,BE、CE分别交AD于点F、G,BC=6,AF:FG:GD=3:2:1,则AB的长为( ) 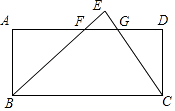
A.1
B.![]()
C.![]()
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径作半圆O交BC于点D,过点D作DE⊥AC,垂足为E. 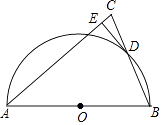
(1)求证:DE是⊙O的切线;
(2)若CE=1,BC=6,求半圆O的半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个25米长的梯子AB,斜靠在一竖直的墙AO上,这时的AO距离为24米,如果梯子的顶端A沿墙下滑4米,那么梯子底端B也外移4米,对吗?为什么?
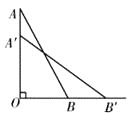
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:已知在△ABC中,边AB上的动点D由A向B运动(与A,B不重合),同时点E由点C沿BC的延长线方向运动(E不与C重合),连接DE交AC于点F,点H是线段AF上一点,求 ![]() 的值.
的值.
(1)初步尝试
如图(1),若△ABC是等边三角形,DH⊥AC,且点D、E的运动速度相等,小王同学发现可以过点D作DG∥BC交AC于点G,先证GH=AH,再证GF=CF,
从而求得 ![]() 的值为 .
的值为 . 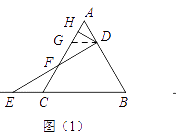
(2)类比探究
如图(2),若△ABC中,∠ABC=90°,∠ADH=∠BAC=30°,且点D,E的运动速度之比是 ![]() :1,求
:1,求 ![]() 的值.
的值.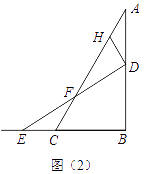
(3)延伸拓展
如图(3)若在△ABC中,AB=AC,∠ADH=∠BAC=36°,记 ![]() =m,且点D、E的运动速度相等,试用含m的代数式表示
=m,且点D、E的运动速度相等,试用含m的代数式表示 ![]() 的值(直接写出果,不必写解答过程).
的值(直接写出果,不必写解答过程).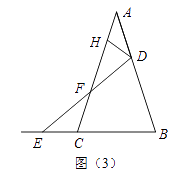
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
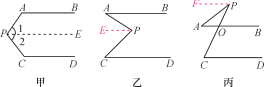
解:过点P作PE∥AB.
∵AB∥CD,
∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).
∴∠1+∠A=180°(两直线平行,同旁内角互补),
∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠1+∠A+∠2+∠C=360°.
又∵∠APC=∠1+∠2,
∴∠APC+∠A+∠C=360°.
如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠P与∠A,∠C之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米).(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08) 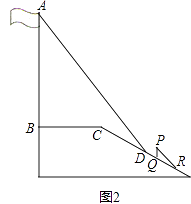
查看答案和解析>>
科目:初中数学 来源: 题型:
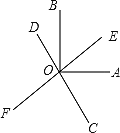
【题目】如图,直线EF、CD相交于点O,OA⊥OB,OC平分∠AOF.
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=30°,请直接写出∠BOD的度数;
(3)观察(1)(2)的结果,猜想∠AOE和∠BOD的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com