
【题目】某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米).(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08) 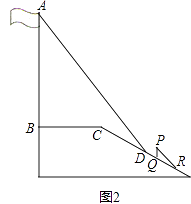
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】同时点燃甲乙两根蜡烛,蜡烛燃烧剩下的长度y(cm)与燃烧时间x(min)的关系如图所示. 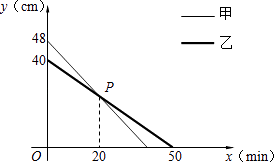
(1)求乙蜡烛剩下的长度y与燃烧时间x的函数表达式;
(2)求点P的坐标,并说明其实际意义;
(3)求点燃多长时间,甲蜡烛剩下长度是乙蜡烛剩下长度的1.1倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度,他们在A处测得信号塔顶端P的仰角是45°,信号塔底端点Q的仰角为31°,沿水平地面向前走100米到B处,测得信号塔顶端P的仰角是68°,求信号塔PQ的高度.(结果精确到0.1米,参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.48,tan31°≈0.60,sin31°≈0.52,cos31°≈0.86)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABE和△ACF中,EB交AC于点M,交FC于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF.下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中,正确的是_________.(填序号)
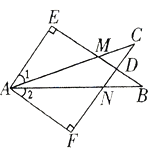
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点E处,连接DE交AB于点F,当△DEB是直角三角形时,DF的长为 . 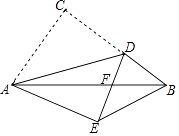
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把两条中线互相垂直的三角形称为“中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均为“中垂三角形”,设BC=a,AC=b,AB=c.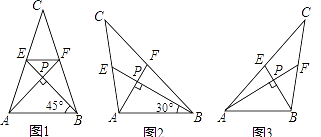
(1)【特例探索】
如图1,当∠ABE=45°,c=2 ![]() 时,a= , b=;如图2,当∠ABE=30°,c=4时,a= , b=;
时,a= , b=;如图2,当∠ABE=30°,c=4时,a= , b=;
(2)【归纳证明】
请你观察(1)中的计算结果,猜想a2 , b2 , c2三者之间的关系,用等式表示出来,请利用图3证明你发现的关系式;
(3)【拓展应用】
如图4,在ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=2 ![]() ,AB=3.求AF的长.
,AB=3.求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,BC= ![]() .以BC的中点O为圆心的圆分别与AB、AC相切于D、E两点,则
.以BC的中点O为圆心的圆分别与AB、AC相切于D、E两点,则 ![]() 的长为 ( )
的长为 ( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水是人类的生命之源.为了鼓励居民节约用水,相关部门实行居民生活用水阶梯式计量水价政策.若居民每户每月用水量不超过10立方米,每立方米按现行居民生活用水水价收费(现行居民生活用水水价=基本水价+污水处理费);若每户每月用水量超过10立方米,则超过部分每立方米在基本水价基础上加价100%,每立方米污水处理费不变.甲用户4月份用水8立方米,缴水费27.6元;乙用户4月份用水12立方米,缴水费46.3元.(注:污水处理的立方数=实际生活用水的立方数)
(1)求每立方米的基本水价和每立方米的污水处理费各是多少元?
(2)如果某用户7月份生活用水水费计划不超过64元,该用户7月份最多可用水多少立方米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com