
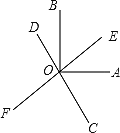
【题目】如图,直线EF、CD相交于点O,OA⊥OB,OC平分∠AOF.
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=30°,请直接写出∠BOD的度数;
(3)观察(1)(2)的结果,猜想∠AOE和∠BOD的数量关系,并说明理由.
【答案】(1)20°(2)15°(3)∠BOD=![]() ∠AOE,理由见解析。
∠AOE,理由见解析。
【解析】
(1)先求出∠AOF,根据角平分线定义求出∠FOC,根据对顶角相等求出∠EOD=∠FOC,求出∠BOE,即可得出答案;
(2)先求出∠AOF,根据角平分线定义求出∠FOC,根据对顶角相等求出∠EOD=∠FOC,求出∠BOE,即可得出答案;
(3)先求出∠AOF,根据角平分线定义求出∠FOC,根据对顶角相等求出∠EOD=∠FOC,求出∠BOE,即可得出答案.
解:(1)∵∠AOE+∠AOF=180°,∠AOE=40°,
∴∠AOF=140°;
又∵OC平分∠AOF,
∴∠FOC=![]() ∠AOF=70°,
∠AOF=70°,
∴∠EOD=∠FOC=70°;
∵OA⊥OB, ∴∠AOB=90°
∵∠BOE=∠AOB-∠AOE=50°,
∴∠BOD=∠EOD-∠BOE=20°;
(2)∵∠AOE+∠AOF=180°,∠AOE=30°,
∴∠AOF=150°;
又∵OC平分∠AOF,
∴∠FOC=![]() ∠AOF=75°,
∠AOF=75°,
∴∠EOD=∠FOC=75°;
∵∠BOE=∠AOB-∠AOE=60°,
∴∠BOD=∠EOD-∠BOE=15°;
(3)从(1)(2)的结果中能看出∠BOD=![]() ∠AOE,理由如下:
∠AOE,理由如下:
∵∠AOE+∠AOF=180°,
∴∠AOF=180°-∠AOE;
又∵OC平分∠AOF,
∴∠FOC=![]() ∠AOF=90°-
∠AOF=90°-![]() ∠AOE,
∠AOE,
∴∠EOD=∠FOC=90°-![]() ∠AOE;
∠AOE;
∵OA⊥OB, ∴∠AOB=90°
∵∠BOE=∠AOB-∠AOE=90°-∠AOE,
∴∠BOD=∠EOD-∠BOE=(90°-![]() ∠AOE)-(90°-∠AOE)=
∠AOE)-(90°-∠AOE)=![]() ∠AOE;
∠AOE;
∴∠BOD=![]() ∠AOE;
∠AOE;


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度,他们在A处测得信号塔顶端P的仰角是45°,信号塔底端点Q的仰角为31°,沿水平地面向前走100米到B处,测得信号塔顶端P的仰角是68°,求信号塔PQ的高度.(结果精确到0.1米,参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.48,tan31°≈0.60,sin31°≈0.52,cos31°≈0.86)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,BC= ![]() .以BC的中点O为圆心的圆分别与AB、AC相切于D、E两点,则
.以BC的中点O为圆心的圆分别与AB、AC相切于D、E两点,则 ![]() 的长为 ( )
的长为 ( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水是人类的生命之源.为了鼓励居民节约用水,相关部门实行居民生活用水阶梯式计量水价政策.若居民每户每月用水量不超过10立方米,每立方米按现行居民生活用水水价收费(现行居民生活用水水价=基本水价+污水处理费);若每户每月用水量超过10立方米,则超过部分每立方米在基本水价基础上加价100%,每立方米污水处理费不变.甲用户4月份用水8立方米,缴水费27.6元;乙用户4月份用水12立方米,缴水费46.3元.(注:污水处理的立方数=实际生活用水的立方数)
(1)求每立方米的基本水价和每立方米的污水处理费各是多少元?
(2)如果某用户7月份生活用水水费计划不超过64元,该用户7月份最多可用水多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 与x轴的负半轴交于点A,与y轴交于点B,连结AB.点C
与x轴的负半轴交于点A,与y轴交于点B,连结AB.点C ![]() 在抛物线上,直线AC与y轴交于点D.
在抛物线上,直线AC与y轴交于点D.
(1)求c的值及直线AC的函数表达式;
(2)点P在x轴的正半轴上,点Q在y轴正半轴上,连结PQ与直线AC交于点M,连结MO并延长交AB于点N,若M为PQ的中点.
①求证:△APM∽△AON;
②设点M的横坐标为m , 求AN的长(用含m的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一笔直的沿湖道路 ![]() 上有
上有 ![]() 、
、 ![]() 两个游船码头,观光岛屿
两个游船码头,观光岛屿 ![]() 在码头
在码头 ![]() 北偏东
北偏东 ![]() 的方向,在码头
的方向,在码头 ![]() 北偏西
北偏西 ![]() 的方向,
的方向, ![]()
![]() .游客小张准备从观光岛屿
.游客小张准备从观光岛屿 ![]() 乘船沿
乘船沿 ![]() 回到码头
回到码头 ![]() 或沿
或沿 ![]() 回到码头
回到码头 ![]() ,设开往码头
,设开往码头 ![]() 、
、 ![]() 的游船速度分别为
的游船速度分别为 ![]() 、
、 ![]() ,若回到
,若回到 ![]() 、
、 ![]() 所用时间相等,则
所用时间相等,则 ![]() (结果保留根号).
(结果保留根号).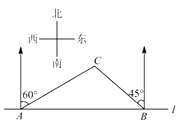
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两直线AB,CD相交于点O,OE平分∠BOD,∠AOC∶∠AOD=7∶11.
(1)求∠COE的度数;
(2)若OF⊥OE,求∠COF的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com