
【题目】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE. 
(1)求证:BD=EC;
(2)若∠E=50°,求∠BAO的大小.
【答案】
(1)证明:∵菱形ABCD,
∴AB=CD,AB∥CD,
又∵BE=AB,
∴BE=CD,BE∥CD,
∴四边形BECD是平行四边形,
∴BD=EC
(2)解:∵平行四边形BECD,
∴BD∥CE,
∴∠ABO=∠E=50°,
又∵菱形ABCD,
∴AC丄BD,
∴∠BAO=90°﹣∠ABO=40°
【解析】(1)根据菱形的对边平行且相等可得AB=CD,AB∥CD,然后证明得到BE=CD,BE∥CD,从而证明四边形BECD是平行四边形,再根据平行四边形的对边相等即可得证;(2)根据两直线平行,同位角相等求出∠ABO的度数,再根据菱形的对角线互相垂直可得AC⊥BD,然后根据直角三角形两锐角互余计算即可得解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,﹣3). 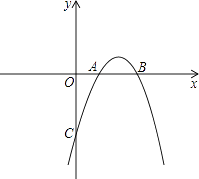
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=﹣x上,并写出平移后抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内时,∠A与∠1+∠2之间有始终不变的关系是( )

A. ∠A=∠1+∠2 B. 2∠A=∠1+∠2 C. 3∠A=∠1+∠2 D. 3∠A=2(∠1+∠2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某镇水库的可用水量为12000万立方米,假设年降水量不变,能维持该镇16万人20年的用水量.实施城市化建设,新迁入4万人后,水库只够维持居民15年的用水量.
(1)问:年降水量为多少万立方米?每人年平均用水量多少立方米?
(2)政府号召节约用水,希望将水库的保用年限提高到25年,则该镇居民人均每年需节约多少立方米才能实现目标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某省是劳务输出大省,农民外出务工增长家庭收入的同时,也一定程度影响了子女的管理和教育,缺少管理和教育的留守儿童的学习和心理健康状况等问题日趋显现,成为社会关注的焦点.该省相关部门就留守儿童学习和心理健康状况等问题进行调查,本次抽样调查了该省某县部分留守儿童,将调查出现的情况分四类,即A类:基本情况正常;B类;有轻度问题;C类:有较为严重问题;D类:有特别严重问题.通过调查,得到下面两幅不完整的统计图,请根据图中的信息解决下面的问题. 
(1)在这次随机抽样调查中,共抽查了多少名学生留守儿童?
(2)扇形统计图中C类所占的圆心角是°;这次调查中为D类的留守儿童有人;
(3)请你估计该县20000名留守儿童中,出现较为严重问题及以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].
(1)如图①,对△ABC作变换[60°, ![]() ]得△AB′C′,则S△AB′C′:S△ABC=;直线BC与直线B′C′所夹的锐角为度;
]得△AB′C′,则S△AB′C′:S△ABC=;直线BC与直线B′C′所夹的锐角为度;
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB′C′,使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值;
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,求θ和n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=ABAD.我们称该四边形为“可分四边形”,∠DAB称为“可分角”.
(1)如图2,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(2)如图3,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则求∠DAB的度数;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,则△DAB的最大面积等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(3)班为了组队参加学校举行的“五水共治”知识竞赛,在班里选取了若干名学生,分成人数相同的甲、乙两组,进行了四次“五水共治”模拟竞赛,成绩优秀的人数和优秀率分别绘制成如图统计图. 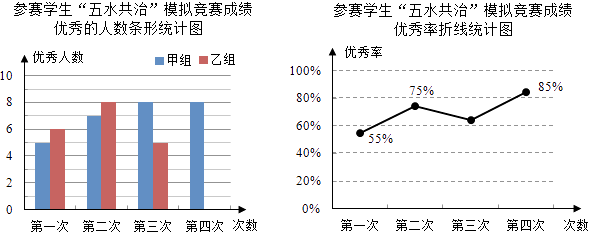
根据统计图,解答下列问题:
(1)第三次成绩的优秀率是多少?并将条形统计图补充完整;
(2)已求得甲组成绩优秀人数的平均数 ![]() =7,方差
=7,方差 ![]() =1.5,请通过计算说明,哪一组成绩优秀的人数较稳定?
=1.5,请通过计算说明,哪一组成绩优秀的人数较稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①, ![]() 是
是![]() 的边
的边![]() 上的高,且
上的高,且![]() cm,
cm,![]() cm,点
cm,点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向终点
向终点![]() 运动,其速度与时间的关系如图②所示,设点
运动,其速度与时间的关系如图②所示,设点![]() 的运动时间为
的运动时间为![]() (s),
(s),![]() 的面积为
的面积为![]() (cm2 ).
(cm2 ).
(1)在点![]() 沿
沿![]() 向点
向点![]() 运动的过程中,它的速度是 cm/s,用含
运动的过程中,它的速度是 cm/s,用含![]() 的代数式表示线段
的代数式表示线段![]() 的长是 cm,变量
的长是 cm,变量![]() 与
与![]() 之间的函数表达式为;
之间的函数表达式为;
(2)当![]() 时,求
时,求![]() 的值.当
的值.当![]() 每增加1时,求
每增加1时,求![]() 的变化情况.
的变化情况.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com