
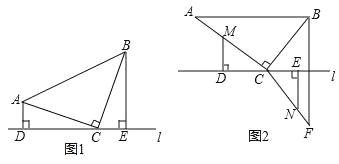
【题目】直角三角形ABC中,∠ACB=90°,直线l过点 C.
(1)当AC=BC时,如图1,分别过点A和B作AD⊥直线l于点D,BE⊥直线l于点 E.△ACD与△CBE是否全等,并说明理由;
(2)当AC=8cm,BC=6cm时,如图2,点B与点F关于直线l对称,连接BF、CF.点M是AC上一点,点N是CF上一点,分别过点M、N作MD⊥直线l于点D,NE⊥直线l于点E,点M从A点出发,以每秒1cm的速度沿A→C路径运动,终点为 C.点N从点F出发,以每秒3cm的速度沿F→C→B→C→F路径运动,终点为F.点M、N同时开始运动,各自达到相应的终点时停止运动,设运动时间为t秒.
①当△CMN为等腰直角三角形时,求t的值;
②当△MDC与△CEN全等时,求t的值.
【答案】(1)全等;证明见解析;(2)①3.5秒或5秒;②3.5秒或5秒或6.5秒.
【解析】
(1)根据垂直的定义得到∠DAC=∠ECB,利用AAS定理证明△ACD≌△CBE;
(2)①分点F沿C→B路径运动和点F沿B→C路径运动两种情况,根据等腰三角形的定义列出算式,计算即可;
②分点F沿F→C路径运动,点F沿C→B路径运动,点F沿B→C路径运动,点F沿C→F路径运动四种情况,根据全等三角形的判定定理列式计算.
解:(1)△ACD与△CBE全等.
理由如下:∵AD⊥直线l,
∴∠DAC+∠ACD=90°,
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∴∠DAC=∠ECB,
在△ACD和△CBE中,
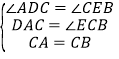 ,
,
∴△ACD≌△CBE(AAS);
(2)①由题意得,AM=t,FN=3t,
则CM=8﹣t,
由折叠的性质可知,CF=CB=6,
∴CN=6﹣3t,
点N在BC上时,△CMN为等腰直角三角形,
当点F沿C→B路径运动时,由题意得,8﹣t=3t﹣6,
解得,t=3.5,
当点F沿B→C路径运动时,由题意得,8﹣t=18﹣3t,
解得,t=5,
综上所述,当t=3.5秒或5秒时,△CMN为等腰直角三角形;
②由折叠的性质可知,∠BCE=∠FCE,
∵∠MCD+∠CMD=90°,∠MCD+∠BCE=90°,
∴∠NCE=∠CMD,
∴当CM=CN时,△MDC与△CEN全等,
当点F沿F→C路径运动时,8﹣t=6﹣3t,
解得,t=﹣1(不合题意),
当点F沿C→B路径运动时,8﹣t═3t﹣6,
解得,t=3.5,
当点F沿B→C路径运动时,由题意得,8﹣t=18﹣3t,
解得,t=5,
当点F沿C→F路径运动时,由题意得,8﹣t=3t﹣18,
解得,t=6.5,
综上所述,当t=3.5秒或5秒或6.5秒时,△MDC与△CEN全等.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).

(1)写出点A、B的坐标:
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′(,)、B′(,)、C′(,).
(3)△ABC的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( ) 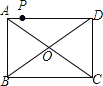
A.4.8
B.5
C.6
D.7.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,射线EP交 ![]() 于点F,交过点C的切线于点D.
于点F,交过点C的切线于点D.
(1)求证:DC=DP;
(2)若∠CAB=30°,当F是 ![]() 的中点时,判断以A,O,C,F为顶点的四边形是什么特殊四边形?说明理由.
的中点时,判断以A,O,C,F为顶点的四边形是什么特殊四边形?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣2ax+c(a<0)的最大值为4,且抛物线过点( ![]() ,﹣
,﹣ ![]() ),点P(t,0)是x轴上的动点,抛物线与y轴交点为C,顶点为D.
),点P(t,0)是x轴上的动点,抛物线与y轴交点为C,顶点为D.
(1)求该二次函数的解析式,及顶点D的坐标;
(2)求|PC﹣PD|的最大值及对应的点P的坐标;
(3)设Q(0,2t)是y轴上的动点,若线段PQ与函数y=a|x|2﹣2a|x|+c的图象只有一个公共点,求t的取值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只蚂蚁在正方形ABCD区域内爬行,点O是对角线的交点,∠MON=90°,OM,ON分别交线段AB,BC于M,N两点,则蚂蚁停留在阴影区域的概率为 . 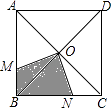
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,把横纵坐标都是整数的点称为“整点”. 
(1)直接写出函数y= ![]() 图象上的所有“整点”A1 , A2 , A3 , …的坐标;
图象上的所有“整点”A1 , A2 , A3 , …的坐标;
(2)在(1)的所有整点中任取两点,用树状图或列表法求出这两点关于原点对称的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校男子足球队的年龄分布如图所示,则根据图中信息可知这些队员年龄的平均数,中位数分别是( ) 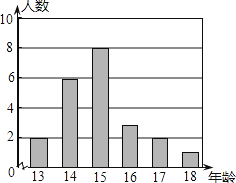
A.15.5,15.5
B.15.5,15
C.15,15.5
D.15,15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设(2y﹣z):(z+2x):y=1:5:2,则(3y﹣z):(2z﹣x):(x+3y)=( )
A.1:5:7
B.3:5:7
C.3:5:8
D.2:5:8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com