
【题目】已知二次函数y=ax2﹣2ax+c(a<0)的最大值为4,且抛物线过点( ![]() ,﹣
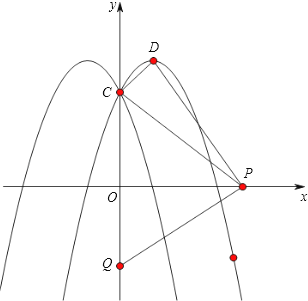
,﹣ ![]() ),点P(t,0)是x轴上的动点,抛物线与y轴交点为C,顶点为D.
),点P(t,0)是x轴上的动点,抛物线与y轴交点为C,顶点为D.
(1)求该二次函数的解析式,及顶点D的坐标;
(2)求|PC﹣PD|的最大值及对应的点P的坐标;
(3)设Q(0,2t)是y轴上的动点,若线段PQ与函数y=a|x|2﹣2a|x|+c的图象只有一个公共点,求t的取值.
【答案】
(1)
解:∵y=ax2﹣2ax+c的对称轴为:x=﹣ ![]() =1,
=1,
∴抛物线过(1,4)和( ![]() ,﹣
,﹣ ![]() )两点,
)两点,
代入解析式得: 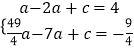 ,
,
解得:a=﹣1,c=3,
∴二次函数的解析式为:y=﹣x2+2x+3,
∴顶点D的坐标为(1,4);
(2)
解:∵C、D两点的坐标为(0,3)、(1,4);
由三角形两边之差小于第三边可知:
|PC﹣PD|≤|CD|,
∴P、C、D三点共线时|PC﹣PD|取得最大值,此时最大值为,
|CD|= ![]() ,
,
由于CD所在的直线解析式为y=x+3,
将P(t,0)代入得t=﹣3,
∴此时对应的点P为(﹣3,0)
(3)
解:y=a|x|2﹣2a|x|+c的解析式可化为:
y= ![]()
设线段PQ所在的直线解析式为y=kx+b,将P(t,0),Q(0,2t)代入得:
线段PQ所在的直线解析式:y=﹣2x+2t,
∴①当线段PQ过点(0,3),即点Q与点C重合时,线段PQ与函数
y= ![]() 有一个公共点,此时t=
有一个公共点,此时t= ![]() ,
,
当线段PQ过点(3,0),即点P与点(3,0)重合时,t=3,此时线段PQ与
y= ![]() 有两个公共点,所以当
有两个公共点,所以当 ![]() ≤t<3时,
≤t<3时,
线段PQ与y= ![]() 有一个公共点,
有一个公共点,
②将y=﹣2x+2t代入y=﹣x2+2x+3(x≥0)得:
﹣x2+2x+3=﹣2x+2t,
﹣x2+4x+3﹣2t=0,
令△=16﹣4(﹣1)(3﹣2t)=0,
t= ![]() >0,
>0,
所以当t= ![]() 时,线段PQ与y=
时,线段PQ与y= ![]() 也有一个公共点,
也有一个公共点,
③当线段PQ过点(﹣3,0),即点P与点(﹣3,0)重合时,线段PQ只与
y=﹣x2﹣2x+3(x<0)有一个公共点,此时t=﹣3,
所以当t≤﹣3时,线段PQ与y= ![]() 也有一个公共点,
也有一个公共点,
综上所述,t的取值是 ![]() ≤t<3或t=
≤t<3或t= ![]() 或t≤﹣3.
或t≤﹣3.
【解析】(1)先利用对称轴公式x=﹣ ![]() 计算对称轴,即顶点坐标为(1,4),再将两点代入列二元一次方程组求出解析式;
计算对称轴,即顶点坐标为(1,4),再将两点代入列二元一次方程组求出解析式;
(2)根据三角形的三边关系:可知P、C、D三点共线时|PC﹣PD|取得最大值,求出直线CD与x轴的交点坐标,就是此时点P的坐标;
(3)先把函数中的绝对值化去,可知y= 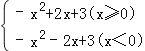 ,此函数是两个二次函数的一部分,分三种情况进行计算:①当线段PQ过点(0,3),即点Q与点C重合时,两图象有一个公共点,当线段PQ过点(3,0),即点P与点(3,0)重合时,两函数有两个公共点,写出t的取值;②线段PQ与当函数y=a|x|2﹣2a|x|+c(x≥0)时有一个公共点时,求t的值;③当线段PQ过点(﹣3,0),即点P与点(﹣3,0)重合时,线段PQ与当函数y=a|x|2﹣2a|x|+c(x<0)时也有一个公共点,则当t≤﹣3时,都满足条件;综合以上结论,得出t的取值.本题考查了二次函数的综合应用,先利用待定系数法求解析式,同时把最大值与三角形的三边关系联系在一起;同时对于二次函数利用动点求取值问题,从特殊点入手,把函数分成几部分考虑,按自变量从大到小的顺序或从小到大的顺序求解.
,此函数是两个二次函数的一部分,分三种情况进行计算:①当线段PQ过点(0,3),即点Q与点C重合时,两图象有一个公共点,当线段PQ过点(3,0),即点P与点(3,0)重合时,两函数有两个公共点,写出t的取值;②线段PQ与当函数y=a|x|2﹣2a|x|+c(x≥0)时有一个公共点时,求t的值;③当线段PQ过点(﹣3,0),即点P与点(﹣3,0)重合时,线段PQ与当函数y=a|x|2﹣2a|x|+c(x<0)时也有一个公共点,则当t≤﹣3时,都满足条件;综合以上结论,得出t的取值.本题考查了二次函数的综合应用,先利用待定系数法求解析式,同时把最大值与三角形的三边关系联系在一起;同时对于二次函数利用动点求取值问题,从特殊点入手,把函数分成几部分考虑,按自变量从大到小的顺序或从小到大的顺序求解.


科目:初中数学 来源: 题型:
【题目】为了丰富学生课外小组活动,培养学生动手操作能力,王老师让学生把5m长的彩绳截成2m或1m的彩绳,用来做手工编织,在不造成浪费的前提下,你有几种不同的截法( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为调查本校学生周末平均每天做作业所用时间的情况,随机调查了50名同学,下图是根据调查所得数据绘制的统计图的一部分.

请根据以上信息,解答下列问题:
(1)在这次调查的数据中,做作业所用时间的众数是 ,中位数是 ,平均数是 ;
(2)若该校共有2000名学生,根据以上调查结果估计该校全体学生每天做作业时间在3小时内(含3小时)的同学共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠B=90°,AB=AD=5,BC=4,M、N、E分别是AB、AD、CB上的点,AM=CE=1,AN=3,点P从点M出发,以每秒1个单位长度的速度沿折线MB﹣BE向点E运动,同时点Q从点N出发,以相同的速度沿折线ND﹣DC﹣CE向点E运动,当其中一个点到达后,另一个点也停止运动.设△APQ的面积为S,运动时间为t秒,则S与t函数关系的大致图象为( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2﹣6x+c与x轴交于点A(﹣5,0)、B(﹣1,0),与y轴交于点C(0,﹣5),点P是抛物线上的动点,连接PA、PC,PC与x轴交于点D.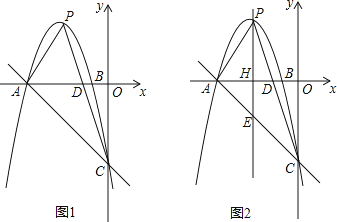
(1)求该抛物线所对应的函数解析式;
(2)若点P的坐标为(﹣2,3),请求出此时△APC的面积;
(3)过点P作y轴的平行线交x轴于点H,交直线AC于点E,如图2.
①若∠APE=∠CPE,求证: ![]() ;
;
②△APE能否为等腰三角形?若能,请求出此时点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
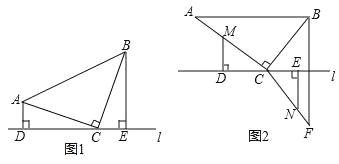
【题目】直角三角形ABC中,∠ACB=90°,直线l过点 C.
(1)当AC=BC时,如图1,分别过点A和B作AD⊥直线l于点D,BE⊥直线l于点 E.△ACD与△CBE是否全等,并说明理由;
(2)当AC=8cm,BC=6cm时,如图2,点B与点F关于直线l对称,连接BF、CF.点M是AC上一点,点N是CF上一点,分别过点M、N作MD⊥直线l于点D,NE⊥直线l于点E,点M从A点出发,以每秒1cm的速度沿A→C路径运动,终点为 C.点N从点F出发,以每秒3cm的速度沿F→C→B→C→F路径运动,终点为F.点M、N同时开始运动,各自达到相应的终点时停止运动,设运动时间为t秒.
①当△CMN为等腰直角三角形时,求t的值;
②当△MDC与△CEN全等时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知A(a,0),B (0,b)分别为两坐标轴上的点,且a,b满足a2﹣24a+|b﹣12|=﹣144,且3OC=OA.
(1)求A、B、C三点的坐标;
(2)若D(2,0),过点D的直线分别交AB、BC于E、F两点,且DF=DE,设E、F两点的横坐标分别为xE、xP,求xE+xP的值;
(3)如图2,若M(4,8),点P是x轴上A点右侧一动点,AH⊥PM于点H,在HM上取点G,使HG=HA,连接CG,当点P在点A右侧运动时,∠CGM的度数是否改变?若不变,请求其值;若改变,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳市政府计划投资1.4万亿元实施东进战略.为了解深圳市民对东进战略的关注情况.某校数学兴趣小组随机采访部分深圳市民,对采访情况制作了统计图表的一部分如下:
关注情况 | 频数 | 频率 |
A.高度关注 | M | 0.1 |
B.一般关注 | 100 | 0.5 |
C.不关注 | 30 | N |
D.不知道 | 50 | 0.25 |

(1)根据上述统计图可得此次采访的人数为人,m= , n=
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,请估计在15000名深圳市民中,高度关注东进战略的深圳市民约有人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com