
【题目】画图(要求:以下操作均只使用无刻度的直尺)
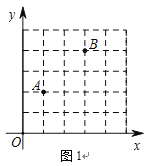
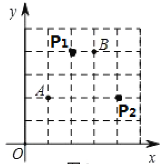
(1)在直角坐标系中我们把横、纵坐标都为整数的点称为整点.如图1中点A(1,2)、B(3,4),在图1中第一象限内找出所有的整点P(图上标为P1、P2),使得点P横、纵坐标的平方和等于20.
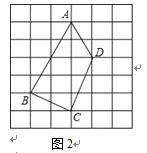
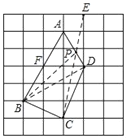
(2)如图2,是大小相等的边长为1的正方形构成的网格,A、B、C、D均为格点.请在线段AD上找一点P,并连结BP使得直线BP将四边形ABCD的面积分为1:2两部分,在图中画出线段BP,并简要说明你的画图方法.
【答案】(1)见解析;(2)见解析.
【解析】
(1)设P(x,y),由题意得x2+y2=20,求出整数即可解决问题;(2)连接BD,先求出△ABD的面积与四边形ABCD的面积,由BQ使得直线BQ将四边形ABCD的面积分为1:2两部分得出△ABP的面积为![]() ,得出即S△ABD=
,得出即S△ABD=![]() S△ABD,也是AP:PD=5:3,所以连接CE,交AD于点P,连接BP,BP为 所求.
S△ABD,也是AP:PD=5:3,所以连接CE,交AD于点P,连接BP,BP为 所求.
解:(1)设P(x,y),由题意得x2+y2=20,
∴x=4,y=2,或者x=2,y=4.
在直角坐标系表示为:
(2)如图,连接BD,则△ABD的面积=△ADF的面积+△BDF的面积=4,
四边形ABCD的面积=△ACD的面积+△ACB的面积=![]() +
+![]() ×5×2=
×5×2=![]() ,
,
∵直线BP将四边形ABCD的面积分为1:2两部分,
∴△ABP的面积=![]() ×
×![]() =
=![]() ,即S△ABD=
,即S△ABD=![]() S△ABD,∴AP:PD=5:3,
S△ABD,∴AP:PD=5:3,
如图,连接CE,交AD于点P,连接BP,则![]() ,
,
∴线段BP即为所求.


科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=10,弦AC=6,∠ACB的平分线交⊙O于点D,过点D作DE∥AB交CA延长线于点E,连接AD,BD.
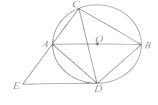
(1)△ABD的面积是________:
(2)求证:DE是⊙O的切线:
(3)求线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
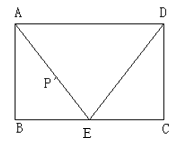
【题目】已知矩形![]() 中,
中,![]() 米,
米,![]() 米,
米,![]() 为
为![]() 中点,动点
中点,动点![]() 以2米/秒的速度从
以2米/秒的速度从![]() 出发,沿着
出发,沿着![]() 的边,按照A
的边,按照A![]() E
E![]() D
D![]() A顺序环行一周,设
A顺序环行一周,设![]() 从
从![]() 出发经过
出发经过![]() 秒后,
秒后,![]() 的面积为
的面积为![]() (平方米),求
(平方米),求![]() 与
与![]() 间的函数关系式.
间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明袋子中有1个红球和n个白球,这些球除颜色外无其他差别.
(1)从袋中随机摸出一个球,记录其颜色,然后放回.大量重复该实验,发现摸到红球的频率稳定于0.25,求n的值.
(2)在(1)的条件下,从袋中随机摸出两个球,求两个球颜色不同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
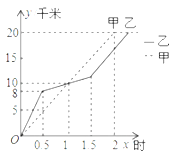
【题目】在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图象信息,下列说法:①两人相遇前,甲速度一直小于乙速度;②出发后1小时,两人行程均为10km;③出发后1.5小时,甲的行程比乙多3km;④甲比乙先到达终点.其中正确的说法是_________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线![]() 的一部分,如图
的一部分,如图
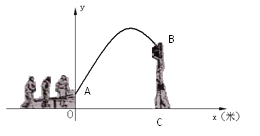
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
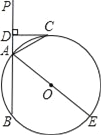
【题目】如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
(1)求证:CD为⊙O的切线;
(2)若DC+DA=6,⊙O的直径为10,求AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
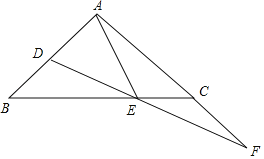
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D,E分别在AB,BC上,∠EAD=∠EDA,点F为DE的延长线与AC的延长线的交点.
(1)求证:DE=EF;
(2)判断BD和CF的数量关系,并说明理由;
(3)若AB=3,AE=![]() ,求BD的长.
,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3).
(1)求抛物线的解析式;
(2)如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;
(3)如图2,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com