
【题目】已知矩形![]() 中,
中,![]() 米,
米,![]() 米,
米,![]() 为
为![]() 中点,动点
中点,动点![]() 以2米/秒的速度从
以2米/秒的速度从![]() 出发,沿着
出发,沿着![]() 的边,按照A
的边,按照A![]() E
E![]() D
D![]() A顺序环行一周,设
A顺序环行一周,设![]() 从
从![]() 出发经过
出发经过![]() 秒后,
秒后,![]() 的面积为
的面积为![]() (平方米),求
(平方米),求![]() 与
与![]() 间的函数关系式.
间的函数关系式.
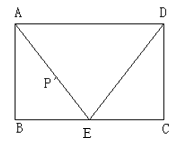
【答案】当点P在线段AE上时,y=![]() ;点P在线段ED上时,y=
;点P在线段ED上时,y=![]() ;点P在线段AD上时, y=32-4x.
;点P在线段AD上时, y=32-4x.
【解析】
分别求出当点P在线段AE上时,点P在线段ED上时,点P在线段AD上时,△ABP的边AB上的高,根据三角形的面积公式可得![]() 与
与![]() 间的函数关系式;
间的函数关系式;
解:∵![]() ,
,![]() 是
是![]() 中点
中点
∴![]()
当![]() ,即
,即![]() 在
在![]() 上时,
上时,
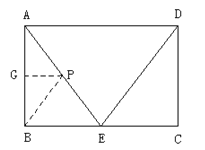
过![]() 作
作![]() ,则
,则![]()
∴△AGP∽△ABE
∴![]() ,∴
,∴![]() ,
,
∴![]()
∴![]() ;
;
当![]() ,即
,即![]() 在
在![]() 上时,AE+EP=2x,DP=10-2x,
上时,AE+EP=2x,DP=10-2x,
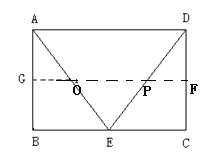
过![]() 作
作![]() 于G,交AE于O,交CD于F,则
于G,交AE于O,交CD于F,则![]() ,
,
∵四边形ABCD是矩形,
∴∠B=∠C=90°,AB=DC,AD=BC.
∵E为BC中点,
∴BE=EC.
∴△ABE≌△DCE.
∴AE=DE=5,
∵PG∥BE
∴△DPF∽△DEC
∴![]() ,即
,即![]()
∴PF=![]() ,
,
∴PG=6-(![]() )=
)=![]() ,
,
∴![]() ,即y=
,即y=![]() ;
;
当![]() ,即
,即![]() 在
在![]() 上时,AE+DE+DP=2x,AP=16-2x,
上时,AE+DE+DP=2x,AP=16-2x,
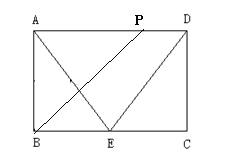
![]() ,
,
即y=32-4x.
故答案为:当点P在线段AE上时,y=![]() ;点P在线段ED上时,y=
;点P在线段ED上时,y=![]() ;点P在线段AD上时, y=32-4x.
;点P在线段AD上时, y=32-4x.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD和正方形AEFG中,边AE在边AB上,AB=![]() ,AE=1.将正方形AEFG绕点A逆时针旋转,设BE的延长线交直线DG于点P,当点P,G第一次重合时停止旋转.在这个过程中:
,AE=1.将正方形AEFG绕点A逆时针旋转,设BE的延长线交直线DG于点P,当点P,G第一次重合时停止旋转.在这个过程中:
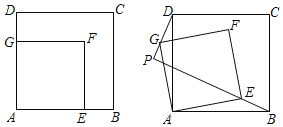
(1)∠BPD=______度;
(2)点P所经过的路径长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
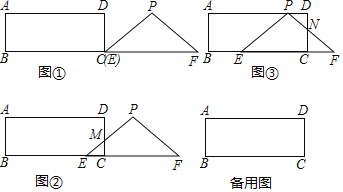
【题目】已知:Rt△EFP和矩形ABCD如图①摆放(点C与点E重合),点B,C(E),F在同一直线上,AB=3cm,BC=9cm,EF=8cm,PE=PF=5cm,如图②,△EFP从图①的位置出发,沿CB方向匀速运动,速度为2cm/s,当点F与点C重合时△EFP停止运动停止.设运动时间为t(s)(0<t<4),解答下列问题:
(1)当0<t<2时,EP与CD交于点M,请用含t的代数式表示CE=______,CM=______;
(2)当2<t<4时,如图③,PF与CD交于点N,设四边形EPNC的面积为y(cm2),求y与t之间的函数关系式;
(3)当2<t<4时,且S四边形EPNC:S矩形ABCD=1:4时,请求出t的值;
(4)连接BD,在运动过程中,当BD与EP相交时,设交点为O,当t=______时;O在∠BAD的平分线上.(不需要写解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
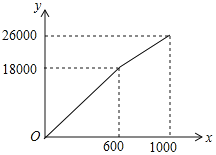
【题目】为了创建“全国文明城市”,鄂州市积极主动建设美丽家园,某社区拟将一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草面积为x(m2),种草费用y1(元)与x(m2)的函数关系式为y1=![]() ,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系如表所示:
,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系如表所示:
x(m2) | 100 | 200 | 300 |
y2(元) | 3900 | 7600 | 11100 |
(1)请直接写出y1与种草面积x(m2)的函数关系式,y2与栽花面积x(m2)的函数关系式;
(2)设这块1000m2空地的绿化总费用为W(元),请利用W与种草面积x(m2)的函数关系式,求出绿化总费用W的最大值;
(3)若种草部分的面积不少于600m2,栽花部分的面积不少于200m2,请求出绿化总费用W的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
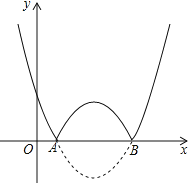
【题目】抛物线y=![]() x2-mx+
x2-mx+![]() m2-2(m为大于0的常数)与x轴交于A,B两点(点A在点B的左侧)
m2-2(m为大于0的常数)与x轴交于A,B两点(点A在点B的左侧)
(1)若点A的坐标为(1,0)
①求抛物线的表达式;
②当n≤x≤2时,函数值y的取值范围是-![]() ≤y≤5-n,求n的值;
≤y≤5-n,求n的值;
(2)将抛物线在x轴下方的部分沿x轴翻折,得到新的函数的图象,如图,当2<x<3时,若此函数的值随x的增大而减小,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
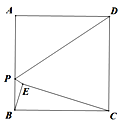
【题目】如图,正方形ABCD的边长为6,点E是正方形内部一点,连接BE,CE,且∠ABE=∠BCE,点P是边AB上一动点,连接PD,PE,则PD+PE的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 蜡烛在真空中燃烧是一个随机事件
B. 在射击比赛中,运动员射中靶心和没有射中靶心的可能性相同
C. 某抽奖游戏的中奖率为![]() ,说明只有抽奖100次,才能中奖1次
,说明只有抽奖100次,才能中奖1次
D. 天气预报明天降水概率为![]() ,表示明天下雨的可能性较大
,表示明天下雨的可能性较大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图(要求:以下操作均只使用无刻度的直尺)
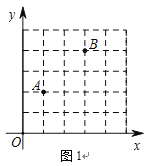
(1)在直角坐标系中我们把横、纵坐标都为整数的点称为整点.如图1中点A(1,2)、B(3,4),在图1中第一象限内找出所有的整点P(图上标为P1、P2),使得点P横、纵坐标的平方和等于20.
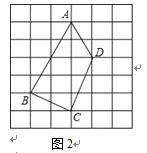
(2)如图2,是大小相等的边长为1的正方形构成的网格,A、B、C、D均为格点.请在线段AD上找一点P,并连结BP使得直线BP将四边形ABCD的面积分为1:2两部分,在图中画出线段BP,并简要说明你的画图方法.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com