
【题目】如图,在正方形ABCD和正方形AEFG中,边AE在边AB上,AB=![]() ,AE=1.将正方形AEFG绕点A逆时针旋转,设BE的延长线交直线DG于点P,当点P,G第一次重合时停止旋转.在这个过程中:
,AE=1.将正方形AEFG绕点A逆时针旋转,设BE的延长线交直线DG于点P,当点P,G第一次重合时停止旋转.在这个过程中:
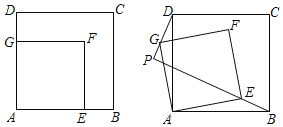
(1)∠BPD=______度;
(2)点P所经过的路径长为______.
【答案】90. ![]()
【解析】
(1)根据正方形性质证△EAB≌△GAD(SAS),得∠ABE=∠ADG,由∠ABE+∠AOB=90°,∠AOB=∠DOP,得∠DOP+∠ADG=90°;(2)当P、G重合时,作AH⊥BG于H.点P经过路径是图中弧AG.根据三角函数知识,求出∠ABH=30°,∠AOG=2∠ABG=60°,![]() 的长=
的长=![]() .
.
解:(1)如图1中,设AD交PB于点O.
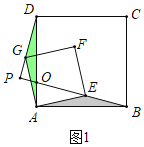
∵四边形ABCD,四边形AEFG都是正方形,
∴AB=AD,AE=AG,∠DAB=∠GAE,
∴∠EAB=∠GAD,
∴△EAB≌△GAD(SAS),
∴∠ABE=∠ADG,
∵∠ABE+∠AOB=90°,∠AOB=∠DOP,
∴∠DOP+∠ADG=90°,
∴∠BPD=90°.
故答案为90.
(2)如图2中,当P、G重合时,作AH⊥BG于H.
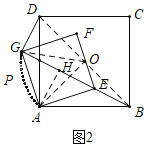
∵∠BPD=90°,
∴点P经过路径是图中弧AG.
∵AE=AG=1,∠EAG=90°,
∴EG=![]() ,
,
∵AH⊥EG,
∴HG=HE,
∴AH=![]() ,
,
∴sin∠ABH=![]() ,
,
∴∠ABH=30°,
∴∠AOG=2∠ABG=60°,
∴![]() 的长=
的长=![]() .
.
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,小巷左右两侧是竖直的墙,一架梯子AC斜靠在右墙,测得梯子顶端距离地面AB=2米,梯子与地面夹角α的正弦值sinα=0.8.梯子底端位置不动,将梯子斜靠在左墙时,顶端距离地面2.4米,则小巷的宽度为( )
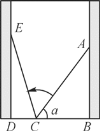
A. 0.7米B. 1.5米
C. 2.2米D. 2.4米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程(x-3)(x-5)=m(m>0)有两个实数根![]() ,
,![]() (
( ![]() <
<![]() ),则下列选项正确的是( )
),则下列选项正确的是( )
A. 3<![]() <
<![]() <5 B. 3<
<5 B. 3<![]() <5<
<5<![]() C.
C. ![]() <2<
<2<![]() <5 D.
<5 D. ![]() <3且
<3且![]() >5
>5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,连结EB,交OD于点F.
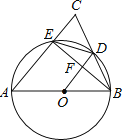
(1)求证:OD⊥BE.
(2)若DE=![]() ,AB=6,求AE的长.
,AB=6,求AE的长.
(3)若△CDE的面积是△OBF面积的![]() ,求线段BC与AC长度之间的等量关系,并说明理由.
,求线段BC与AC长度之间的等量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=OC, 连接 CE、OE,连接AE交OD于点F.(1)求证:OE=CD (2)若菱形ABCD的边长为6,∠ABC=60°,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
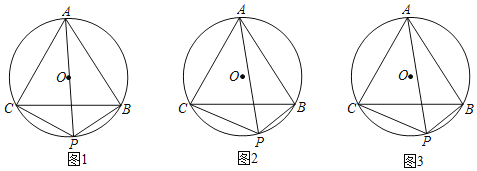
【题目】如图,△ABC是⊙O的内接正三角形,点P在劣弧BC上(不与点B,C重合).
(1)如图1,若PA是⊙O的直径,则PA______PB+PC(请填“>”,“=”或“<”)
(2)如图2,若PA不是⊙O的直径,那么(1)中的结论是否仍成立?如果不成立,请说明理由:如果成立,请给出证明.
(3)如图3,若四边形ACPB的面积是16![]() .
.
①求PA的长;
②设y=S△PCB+![]() S△PCA,求当PC为何值时,y的值最大?并直接写出此时⊙O的半径.
S△PCA,求当PC为何值时,y的值最大?并直接写出此时⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校在倡导学生大课间活动中,随机抽取了部分学生对“我最喜爱课间活动”进行了一次抽样调查,分别从打篮球、踢足球、自由活动、跳绳、其它、等5个方面进行问卷调查(每人只能选一项),根据调查结果绘制了如图的不完整统计图,请你根据图中信息,解答下列问题
(1)本次调查共抽取了学生多少人?
(2)求本次调查中喜欢踢足球人数,并补全条形统计图;
(3)若全校共有中学生1200人,请你估计我校喜欢跳绳学生有多少人.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=10,弦AC=6,∠ACB的平分线交⊙O于点D,过点D作DE∥AB交CA延长线于点E,连接AD,BD.
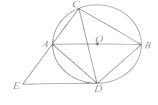
(1)△ABD的面积是________:
(2)求证:DE是⊙O的切线:
(3)求线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
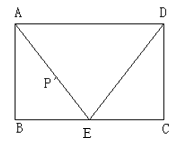
【题目】已知矩形![]() 中,
中,![]() 米,
米,![]() 米,
米,![]() 为
为![]() 中点,动点
中点,动点![]() 以2米/秒的速度从
以2米/秒的速度从![]() 出发,沿着
出发,沿着![]() 的边,按照A
的边,按照A![]() E
E![]() D
D![]() A顺序环行一周,设
A顺序环行一周,设![]() 从
从![]() 出发经过
出发经过![]() 秒后,
秒后,![]() 的面积为
的面积为![]() (平方米),求
(平方米),求![]() 与
与![]() 间的函数关系式.
间的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com