
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,连结EB,交OD于点F.
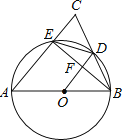
(1)求证:OD⊥BE.
(2)若DE=![]() ,AB=6,求AE的长.
,AB=6,求AE的长.
(3)若△CDE的面积是△OBF面积的![]() ,求线段BC与AC长度之间的等量关系,并说明理由.
,求线段BC与AC长度之间的等量关系,并说明理由.
【答案】(1)证明见解析;(2)4;(3)AC=![]() BC.
BC.
【解析】
(1)连接AD.根据直径所对的圆周角是直角、等腰三角形的性质以及平行线的性质即可证明;
(2)先证△CDE∽△CAB得![]() ,据此求得CE的长,依据AE=AC-CE=AB-CE可得答案;
,据此求得CE的长,依据AE=AC-CE=AB-CE可得答案;
(3)由BD=CD知S△CDE=S△BDE,证△OBF∽△ABE得![]() ,据此知S△ABE=4S△OBF,结合
,据此知S△ABE=4S△OBF,结合![]() 知S△ABE=6S△CDE,S△CAB=8S△CDE,由△CDE∽△CAB知
知S△ABE=6S△CDE,S△CAB=8S△CDE,由△CDE∽△CAB知![]() ,据此得出
,据此得出![]() ,结合BD=CD,AB=AC知
,结合BD=CD,AB=AC知![]() ,从而得出答案.
,从而得出答案.
(1)连接AD,

∵AB是直径,
∴∠AEB=∠ADB=90°,
∵AB=AC,
∴∠CAD=∠BAD,BD=CD,
∴![]() ,
,
∴OD⊥BE;
(2)∵∠AEB=90°,
∴∠BEC=90°,
∵BD=CD,
∴BC=2DE=2![]() ,
,
∵四边形ABDE内接于⊙O,
∴∠BAC+∠BDE=180°,
∵∠CDE+∠BDE=180°,
∴∠CDE=∠BAC,
∵∠C=∠C,
∴△CDE∽△CAB,
∴![]() ,即
,即![]() ,
,
∴CE=2,
∴AE=AC-CE=AB-CE=4;
(3)∵BD=CD,
∴S△CDE=S△BDE,
∵BD=CD,AO=BO,
∴OD∥AC,
∵△OBF∽△ABE,
∴![]() ,
,
∴S△ABE=4S△OBF,
∵![]() ,
,
∴S△ABE=4S△OBF=6S△CDE,
∴S△CAB=S△CDE+S△BDE+S△ABE=8S△CDE,
∵△CDE∽△CAB,
∴![]() ,
,
∴![]() ,
,
∵BD=CD,AB=AC,
∴![]() ,即AC=
,即AC=![]() BC.
BC.


科目:初中数学 来源: 题型:
【题目】下列给出的方程中,属于一元二次方程的是( )
A. x(x﹣1)=6B. x2+![]() =0C. (x﹣3)(x﹣2)=x2D. ax2+bx+c=0
=0C. (x﹣3)(x﹣2)=x2D. ax2+bx+c=0
查看答案和解析>>
科目:初中数学 来源: 题型:
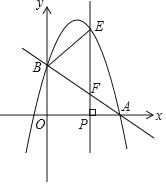
【题目】如图,在平面直角坐标系中,直线y=-![]() x+2分别交x轴、y轴于点A、B,抛物线y=﹣x2+bx+c经过点A、B.点P是x轴上一个动点,过点P作垂直于x轴的直线分别交抛物线和直线AB于点E和点F.设点P的横坐标为m.
x+2分别交x轴、y轴于点A、B,抛物线y=﹣x2+bx+c经过点A、B.点P是x轴上一个动点,过点P作垂直于x轴的直线分别交抛物线和直线AB于点E和点F.设点P的横坐标为m.
(1)点A的坐标为 .
(2)求这条抛物线所对应的函数表达式.
(3)点P在线段OA上时,若以B、E、F为顶点的三角形与△FPA相似,求m的值.
(4)若E、F、P三个点中恰有一点是其它两点所连线段的中点(三点重合除外),称E、F、P三点为“共谐点”.直接写出E、F、P三点成为“共谐点”时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知AB是⊙O 的直径,C是⊙O 上一点,∠ACB的平分线交⊙O 于点D,作PD∥AB,交CA的延长线于点P.连结AD,BD.
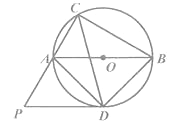
求证:(1)PD是⊙O 的切线;
(2)△PAD![]() △DBC.
△DBC.
查看答案和解析>>
科目:初中数学 来源: 题型:
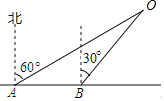
【题目】如图,某轮船在海上向正东方向航行,上午8:00在点A处测得小岛O在北偏东60°方向的16![]() km处;上午8:30轮船到达B处,测得小岛O在北偏东30°方向.
km处;上午8:30轮船到达B处,测得小岛O在北偏东30°方向.
(1)求轮船从A处到B处的航速;
(2)如果轮船按原速继续向东航行,还需经过多少时间轮船才恰好位于小岛的东南方向?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为推动“时刻听党话 永远跟党走”校园主题教育活动,计划开展四项活动:A:党史演讲比赛,B:党史手抄报比赛,C:党史知识竞赛,D:红色歌咏比赛.校团委对学生最喜欢的一项活动进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2两幅不完整的统计图.请结合图中信息解答下列问题:
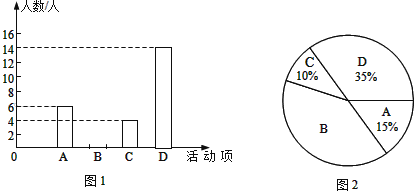
(1)本次共调查了 名学生;
(2)将图1的统计图补充完整;
(3)已知在被调查的最喜欢“党史知识竞赛”项目的4个学生中只有1名女生,现从这4名学生中任意抽取2名学生参加该项目比赛,请用画树状图或列表的方法,求出恰好抽到一名男生一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD和正方形AEFG中,边AE在边AB上,AB=![]() ,AE=1.将正方形AEFG绕点A逆时针旋转,设BE的延长线交直线DG于点P,当点P,G第一次重合时停止旋转.在这个过程中:
,AE=1.将正方形AEFG绕点A逆时针旋转,设BE的延长线交直线DG于点P,当点P,G第一次重合时停止旋转.在这个过程中:
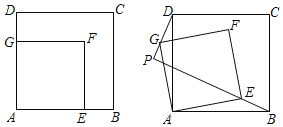
(1)∠BPD=______度;
(2)点P所经过的路径长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示.根据图象所提供的信息有:①甲队挖掘30m时,用了3h;②挖掘6h时甲队比乙队多挖了10m;③乙队的挖掘速度总是小于甲队;④开挖后甲、乙两队所挖河渠长度相等时,x=4.其中一定正确的有( )
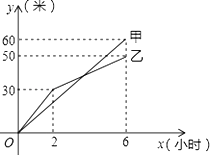
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
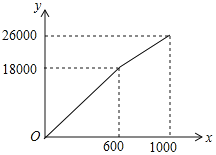
【题目】为了创建“全国文明城市”,鄂州市积极主动建设美丽家园,某社区拟将一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草面积为x(m2),种草费用y1(元)与x(m2)的函数关系式为y1=![]() ,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系如表所示:
,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系如表所示:
x(m2) | 100 | 200 | 300 |
y2(元) | 3900 | 7600 | 11100 |
(1)请直接写出y1与种草面积x(m2)的函数关系式,y2与栽花面积x(m2)的函数关系式;
(2)设这块1000m2空地的绿化总费用为W(元),请利用W与种草面积x(m2)的函数关系式,求出绿化总费用W的最大值;
(3)若种草部分的面积不少于600m2,栽花部分的面积不少于200m2,请求出绿化总费用W的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com