
【题目】下列给出的方程中,属于一元二次方程的是( )
A. x(x﹣1)=6B. x2+![]() =0C. (x﹣3)(x﹣2)=x2D. ax2+bx+c=0
=0C. (x﹣3)(x﹣2)=x2D. ax2+bx+c=0
科目:初中数学 来源: 题型:
【题目】 已知:点A(2016,0)、B(0,2018),以AB为斜边在直线AB下方作等腰直角△ABC,则点C的坐标为( )
A. (2,2 )B. (2,﹣2 )C. (﹣1,1 )D. (﹣1,﹣1 )
查看答案和解析>>
科目:初中数学 来源: 题型:
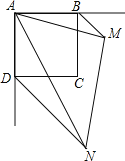
【题目】已知:如图,四边形ABCD是正方形,∠PAQ=45°,将∠PAQ绕着正方形的顶点A旋转,使它与正方形ABCD的两个外角∠EBC和∠FDC的平分线分别交于点M和N,连接MN.
(1)求证:△ABM∽△NDA;
(2)连接BD,当∠BAM的度数为多少时,四边形BMND为矩形,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 xOy 中,已知正比例函数 y1=﹣2x 的图象与反比例函数 y2=![]() 的图象交于 A(﹣1,a),B 两点.
的图象交于 A(﹣1,a),B 两点.
(1)求出反比例函数的解析式及点 B 的坐标;
(2)观察图象,请直接写出满足 y≤2 的取值范围;
(3)点 P 是第四象限内反比例函数的图象上一点,若△POB 的面积为 1,请直接写出点 P的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
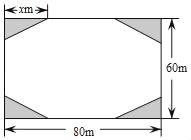
【题目】结合西昌市创建文明城市要求,某小区业主委员会决定把一块长80m,宽60m的矩形空地建成花园小广场,设计方案如图所示,阴影区域为绿化区(四块绿化区为全等的直角三角形),空白区域为活动区,且四周出口宽度一样,其宽度不小于36m,不大于44m,预计活动区造价60元/m2,绿化区造价50元/m2,设绿化区域较长直角边为xm.
(1)用含x的代数式表示出口的宽度;
(2)求工程总造价y与x的函数关系式,并直接写出x的取值范围;
(3)如果业主委员会投资28.4万元,能否完成全部工程?若能,请写出x为整数的所有工程方案;若不能,请说明理由.
(4)业主委员会决定在(3)设计的方案中,按最省钱的一种方案,先对四个绿化区域进行绿化,在实际施工中,每天比原计划多绿化11m2,结果提前4天完成四个区域的绿化任务,问原计划每天绿化多少m2.
查看答案和解析>>
科目:初中数学 来源: 题型:
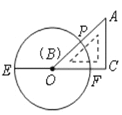
【题目】如图,已知![]() 是
是![]() 的直径,把
的直径,把![]() 为
为![]() 的直角三角板
的直角三角板![]() 的一条直角边
的一条直角边![]() 放在直线
放在直线![]() 上,斜边
上,斜边![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 与点
与点![]() 重合.将三角板
重合.将三角板![]() 沿
沿![]() 方向平移,使得点
方向平移,使得点![]() 与点
与点![]() 重合为止.设
重合为止.设![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小巷左右两侧是竖直的墙,一架梯子AC斜靠在右墙,测得梯子顶端距离地面AB=2米,梯子与地面夹角α的正弦值sinα=0.8.梯子底端位置不动,将梯子斜靠在左墙时,顶端距离地面2.4米,则小巷的宽度为( )
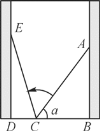
A. 0.7米B. 1.5米
C. 2.2米D. 2.4米
查看答案和解析>>
科目:初中数学 来源: 题型:
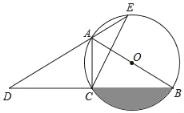
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,延长BC至点D,使得DC=BC,直线DA与⊙O的另一个交点为E,连结AC,CE.
(1)求证:CD=CE;
(2)若AC=2,∠E=30°,求阴影部分(弓形)面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,连结EB,交OD于点F.
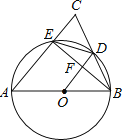
(1)求证:OD⊥BE.
(2)若DE=![]() ,AB=6,求AE的长.
,AB=6,求AE的长.
(3)若△CDE的面积是△OBF面积的![]() ,求线段BC与AC长度之间的等量关系,并说明理由.
,求线段BC与AC长度之间的等量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com