
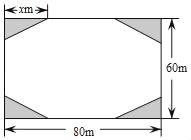
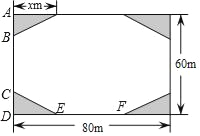
【题目】结合西昌市创建文明城市要求,某小区业主委员会决定把一块长80m,宽60m的矩形空地建成花园小广场,设计方案如图所示,阴影区域为绿化区(四块绿化区为全等的直角三角形),空白区域为活动区,且四周出口宽度一样,其宽度不小于36m,不大于44m,预计活动区造价60元/m2,绿化区造价50元/m2,设绿化区域较长直角边为xm.
(1)用含x的代数式表示出口的宽度;
(2)求工程总造价y与x的函数关系式,并直接写出x的取值范围;
(3)如果业主委员会投资28.4万元,能否完成全部工程?若能,请写出x为整数的所有工程方案;若不能,请说明理由.
(4)业主委员会决定在(3)设计的方案中,按最省钱的一种方案,先对四个绿化区域进行绿化,在实际施工中,每天比原计划多绿化11m2,结果提前4天完成四个区域的绿化任务,问原计划每天绿化多少m2.
【答案】(1)(80﹣2x)cm;(2)y==﹣20x2+200x+288000,18≤x≤22;(3)能,所有方案如下:①较长直角边为20m,短直角边为10m,出口宽度为40m;②较长直角边为21m,短直角边为11m,出口宽度为38m;③较长直角边为22m,短直角边为12m,出口宽度为36m;(4)33m2
【解析】
(1)根据图形可得结论;(2)根据面积×造价可得绿化区和活动区的费用,相加可得y与x的关系式,根据所有长度都是非负数列不等式组可得x的取值范围;(3)业主委员会投资28.4万元,列不等式,结合二次函数的增减性可得结论;(4)先计算设计的方案中,最省钱的一种方案为x=22时,计算绿化面积,根据题意列分式方程可得结论,注意方程要检验.
解:(1)由题意可得,
出口的宽度为;
(2)由题意可得,BC=EF=80﹣2x,
∴AB=CD=![]() =x﹣10,
=x﹣10,
y=50×4×![]() x(x﹣10)+60×[60×80﹣4×
x(x﹣10)+60×[60×80﹣4×![]() x(x﹣10)]=﹣20x2+200x+288000,
x(x﹣10)]=﹣20x2+200x+288000,
∵36≤80﹣2x≤44,
∴18≤x≤22,
(3)﹣20x2+200x+288000≤284000,
x2﹣10x﹣200≥0,
设y=x2﹣10x﹣200=(x﹣5)2﹣225,
当y=0时,x2﹣10x﹣200=0,x=20或﹣10,
∴当y≥0时,x≤﹣10或x≥20
由(2)知:18≤x≤22,
∴20≤x≤22,
所以业主委员会投资28.4万元,能完成全部工程,
所有工程方案如下:①较长直角边为20m,短直角边为10m,出口宽度为40m;
②较长直角边为21m,短直角边为11m,出口宽度为38m;
③较长直角边为22m,短直角边为12m,出口宽度为36m;
(4)y=﹣20x2+200x+288000=﹣20(x﹣5)2+288450,
在20≤x≤22中y随x的增大而减小,
∴当x=22时,y有最小值,
绿化面积=4×![]() ×22×(22﹣10)=528,
×22×(22﹣10)=528,
设原计划每天绿化xm2,则在实际施工中,每天绿化(x+11)m2,
则![]() =4,
=4,
解得:x=33或﹣44(舍),
经检验x=33是原方程的解,
答:原计划每天绿化33m2.


科目:初中数学 来源: 题型:
【题目】为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对A、B两类学校进行改扩建,根据预算,改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元.
(1)改扩建1所A类学校和1所B类学校所需资金分别是多少万元?
(2)该县计划改扩建A、B两类学校共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元,其中地方财政投入到A、B两类学校的改扩建资金分别为每所300万元和500万元.请问共有哪几种改扩建方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
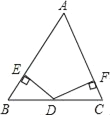
【题目】如图,在△ABC中,AB=AC,D是底边BC的中点,作DE⊥AB于E,DF⊥AC于F
求证:DE=DF.
证明:∵AB=AC,∴∠B=∠C①.
在△BDE和△CDF中,∠B=∠C,∠BED=∠CFD,BD=CD,∴△BDE≌△CDF②.∴DE=DF③.
(1)上面的证明过程是否正确?若正确,请写出①、②和③的推理根据.
(2)请你写出另一种证明此题的方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c与x轴交于A,B两点,顶点C的纵坐标为﹣2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论:①b>0;②a﹣b+c<0;③阴影部分的面积为4;④若c=﹣1,则b2=4a.其中正确的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列给出的方程中,属于一元二次方程的是( )
A. x(x﹣1)=6B. x2+![]() =0C. (x﹣3)(x﹣2)=x2D. ax2+bx+c=0
=0C. (x﹣3)(x﹣2)=x2D. ax2+bx+c=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应香洲区全面推进书香校园建设的号召,班长小青随机调查了若干同学一周课外阅读的时间t(单位:小时),将获得的数据分成四组,绘制了如下统计图(A:0<t≤7,B:7<t≤14,C:14<t≤21,D:t>21),根据图中信息,解答下列问题:

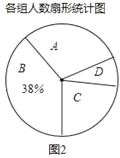
(1)这项工作中被调查的总人数是多少?
(2)补全条形统计图,并求出表示A组的扇形统计图的圆心角的度数;
(3)如果小青想从D组的甲、乙、丙、丁四人中先后随机选择两人做读书心得发言代表,请用列表或树状图的方法求出恰好选中甲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
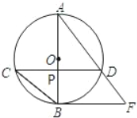
【题目】如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD的延长线交于点F,且∠AFB=∠ABC.
(1)求证:直线BF是⊙O的切线.
(2)若CD=2![]() ,OP=1,求线段BF的长.
,OP=1,求线段BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
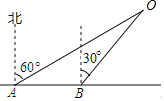
【题目】如图,某轮船在海上向正东方向航行,上午8:00在点A处测得小岛O在北偏东60°方向的16![]() km处;上午8:30轮船到达B处,测得小岛O在北偏东30°方向.
km处;上午8:30轮船到达B处,测得小岛O在北偏东30°方向.
(1)求轮船从A处到B处的航速;
(2)如果轮船按原速继续向东航行,还需经过多少时间轮船才恰好位于小岛的东南方向?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com