
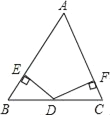
����Ŀ����ͼ������ABC�У�AB��AC��D�ǵױ�BC���е㣬��DE��AB��E��DF��AC��F
��֤��DE��DF��
֤������AB��AC�����B����C�٣�
����BDE����CDF�У���B����C����BED����CFD��BD��CD�����BDE�ա�CDF�ڣ���DE��DF�ۣ�
��1�������֤�������Ƿ���ȷ������ȷ����д���١��ں͢۵��������ݣ�
��2������д����һ��֤������ķ�����
 ��ɢ˼ά�¿���ϵ�д�
��ɢ˼ά�¿���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��һ��ֱ��ˮƽ��Ľ����ijͬѧ�ӽ������B����������ˮƽ������������20�����C���پ���һ���¶ȣ����±ȣ�Ϊi=1��0.75���³�Ϊ10��б��CD�����D��Ȼ������ˮƽ������������40�����E��A��B��C��D��E����ͬһƽ���ڣ�����E����ý����ﶥ��A������Ϊ24����������AB�ĸ߶�ԼΪ���ο����ݣ�sin24���0.41��cos24���0.91��tan24��=0.45����������

A. 21.7�� B. 22.4�� C. 27.4�� D. 28.8��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
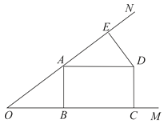
����Ŀ����ͼ����A�ڡ�MON�ı�ON�ϣ�AB��OM��B��AE=OB��DE��ON��E��AD=AO��DC��OM��C��
��1����֤���ı���ABCD�Ǿ��Σ�
��2����DE=3��OE=9����AB��AD�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
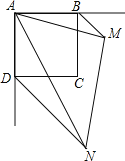
����Ŀ����֪����ͼ���ı���ABCD�������Σ���PAQ��45�㣬����PAQ���������εĶ���A��ת��ʹ����������ABCD��������ǡ�EBC�͡�FDC��ƽ���߷ֱ��ڵ�M��N������MN��
��1����֤����ABM�ס�NDA��
��2������BD������BAM�Ķ���Ϊ����ʱ���ı���BMNDΪ���Σ�������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
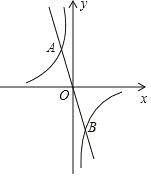
����Ŀ����ͼ����ƽ��ֱ������ϵ xOy �У���֪���������� y1����2x ��ͼ���뷴�������� y2��![]() ��ͼ���� A����1��a����B ���㣮
��ͼ���� A����1��a����B ���㣮
(1)��������������Ľ���ʽ���� B �����ꣻ
(2)�۲�ͼ����ֱ��д������ y��2 ��ȡֵ��Χ��
(3)�� P �ǵ��������ڷ�����������ͼ����һ�㣬����POB �����Ϊ 1����ֱ��д���� P�ĺ����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ xOy �У���֪���������� y1����2x ��ͼ���뷴�������� y2��![]() ��ͼ���� A����1��a����B ���㣮
��ͼ���� A����1��a����B ���㣮
(1)��������������Ľ���ʽ���� B �����ꣻ
(2)�۲�ͼ����ֱ��д������ y��2 ��ȡֵ��Χ��
(3)�� P �ǵ��������ڷ�����������ͼ����һ�㣬����POB �����Ϊ 1����ֱ��д���� P�ĺ����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
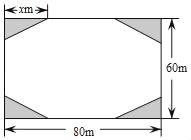
����Ŀ����������д�����������Ҫ��ijС��ҵ��ίԱ�������һ�鳤80m����60m�ľ��οյؽ��ɻ�С�㳡����Ʒ�����ͼ��ʾ����Ӱ����Ϊ�̻������Ŀ��̻���Ϊȫ�ȵ�ֱ�������Σ����հ�����Ϊ����������ܳ��ڿ���һ��������Ȳ�С��36m��������44m��Ԥ�ƻ�����60Ԫ/m2���̻������50Ԫ/m2�����̻�����ϳ�ֱ�DZ�Ϊxm��
��1���ú�x�Ĵ���ʽ��ʾ���ڵĿ��ȣ�
��2���������y��x�ĺ�����ϵʽ����ֱ��д��x��ȡֵ��Χ��
��3�����ҵ��ίԱ��Ͷ��28.4��Ԫ���ܷ����ȫ�����̣����ܣ���д��xΪ���������й��̷����������ܣ���˵�����ɣ�
��4��ҵ��ίԱ������ڣ�3����Ƶķ����У�����ʡǮ��һ�ַ������ȶ��ĸ��̻���������̻�����ʵ��ʩ���У�ÿ���ԭ�ƻ����̻�11m2�������ǰ4������ĸ�������̻�������ԭ�ƻ�ÿ���̻�����m2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С��������������ֱ��ǽ��һ������ACб������ǽ��������Ӷ��˾������AB��2�ף����������н���������ֵsin����0.8�����ӵ�λ�ò�����������б������ǽʱ�����˾������2.4�ף���С��Ŀ���Ϊ( )
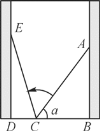
A. 0.7��B. 1.5��
C. 2.2��D. 2.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x�ķ���(x-3)(x-5)=m(m>0)������ʵ����![]() ��
��![]() (
( ![]() <
<![]() )��������ѡ����ȷ���ǣ� ��
)��������ѡ����ȷ���ǣ� ��
A. 3<![]() <
<![]() <5 B. 3<
<5 B. 3<![]() <5<
<5<![]() C.
C. ![]() <2<
<2<![]() <5 D.
<5 D. ![]() <3��
<3��![]() >5
>5
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com