
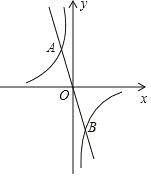
【题目】如图,在平面直角坐标系 xOy 中,已知正比例函数 y1=﹣2x 的图象与反比例函数 y2=![]() 的图象交于 A(﹣1,a),B 两点.
的图象交于 A(﹣1,a),B 两点.
(1)求出反比例函数的解析式及点 B 的坐标;
(2)观察图象,请直接写出满足 y≤2 的取值范围;
(3)点 P 是第四象限内反比例函数的图象上一点,若△POB 的面积为 1,请直接写出点 P的横坐标.
【答案】(1)y=﹣![]() ,B(1,﹣2);(2)x
,B(1,﹣2);(2)x![]() ﹣1 或 x>0;(3)
﹣1 或 x>0;(3)![]() .
.
【解析】
(1)已知点A的坐标代入正比例函数可求出a,再把点A坐标代入可求出反比例函数解析式;又因为正比例函数和反比例函数交点是A、B,可知A、B两点关于原点对称从而可求出B点坐标
(2)观察图像即可得出
(3)根据题意补全图形把三角形的面积转换成梯形的面积然后根据已知求解一元二次方程,把不符合实际情况的根舍掉即可得出答案。
(1)把 A(﹣1,a)代入 y=﹣2x,可得 a=2,
∴A(﹣1,2),
把 A(﹣1,2)代入 y=![]() ,可得 k=﹣2,
,可得 k=﹣2,
∴反比例函数的表达式为 y=﹣![]() ,
,
∵点 B 与点 A 关于原点对称,
∴B(1,﹣2).
(2)∵A(﹣1,2),
∴y≤2 的取值范围是 x![]() ﹣1 或 x>0;
﹣1 或 x>0;
(3)作 BM⊥x 轴于 M,PN⊥x 轴于 N,
∵S 梯形 MBPN=S△POB=1,
设 P(m,﹣![]() ),则
),则![]() ×(2+
×(2+![]() )(m﹣1)=1 或
)(m﹣1)=1 或![]() ×(2+
×(2+![]() )(1﹣m)=1整理得,m2﹣m﹣1=0 或 m2+m+1=0,
)(1﹣m)=1整理得,m2﹣m﹣1=0 或 m2+m+1=0,
解得 m=![]()
∴P 点的横坐标![]()


科目:初中数学 来源: 题型:
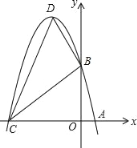
【题目】已知:m,n是方程x2﹣6x+5=0的两个实数根,且m<n,抛物线y=﹣x2+bx+c的图象经过点A(m,0),B(0,n).
(1)求这个抛物线的解析式;
(2)设(1)中的抛物线与x轴的另一交点为C,抛物线的顶点为D,试求出点C,D的坐标和△BCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 和
和![]() ,以下说法:
,以下说法:
①它们的图象都是开口向上;②它们的对称轴都是y轴,顶点坐标都是原点(0,0);③当x>0时,它们的函数y都是随x的增大而增大;④它们的开口的大小是一样的.
其中正确的说法有_______个.
查看答案和解析>>
科目:初中数学 来源: 题型:
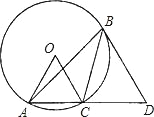
【题目】如图,在⊙O 的内接△ABC 中,∠ABC=30°,AC 的延长线与过点 B 的⊙O 的切线相交于点 D,若⊙O 的半径 OC=1,BD∥OC,则 CD 的长为( )
A. 1+![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
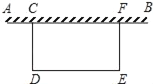
【题目】如图,某校广场有一段25米长的旧围栏,现打算利用该围栏的一部分(或全部)为一边,围成一块100平方米的长方形草坪(如图CDEF,CD<CF)已知整修旧围栏的价格是每米1.75元,建新围栏的价格是4.5元.若CF=x米,计划修建费为y元.
(1)求y与x的函数关系式,并指出x的取值范围;
(2)若计划修建费为150元,能否完成该草坪围栏的修建任务?若能完成,请算出利用旧围栏多少米;若不能完成,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是( )
A. 30° B. 60° C. 30°或150° D. 60°或120°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com