
【题目】在同一平面直角坐标系中,函数y=mx+m与y=![]() m≠0)的图象可能是( )
m≠0)的图象可能是( )
A. 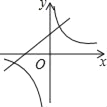 B.
B. 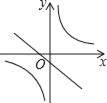 C.
C. 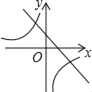 D.
D. 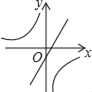
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
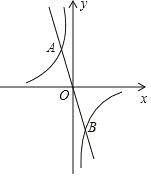
【题目】如图,在平面直角坐标系 xOy 中,已知正比例函数 y1=﹣2x 的图象与反比例函数 y2=![]() 的图象交于 A(﹣1,a),B 两点.
的图象交于 A(﹣1,a),B 两点.
(1)求出反比例函数的解析式及点 B 的坐标;
(2)观察图象,请直接写出满足 y≤2 的取值范围;
(3)点 P 是第四象限内反比例函数的图象上一点,若△POB 的面积为 1,请直接写出点 P的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在倡导“社会主义核心价值观”演讲比赛中,某校根据初赛成绩在七、八年级分别选出10名同学参加决赛,对这些同学的决赛成绩进行整理分析,绘制成如下团体成绩统计表和选手成绩折线统计图:
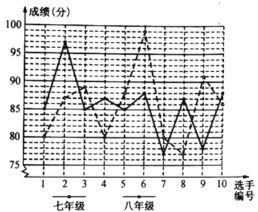
七年级 | 八年级 | |
平均数 | 85.7 | _______ |
众数 | _______ | _______ |
方差 | 37.4 | 27.8 |
根据上述图表提供的信息,解答下列问题:
(1)请你把上面的表格填写完整;
(2)考虑平均数与方差,你认为哪个年级的团体成绩更好?
(3)假设在每个年级的决赛选手中分别选出2个参加决赛,你认为哪个年级的实力更强一些?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.

(1)若AB=4,求弧CD的长.
(2)若弧BC=弧AD,AD=AP. 求证:PD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒中有4个完全相同的小球,把它们分别标号为1,2,3,4,随机摸取一个小球然后放回,再随机摸出一个小球.
(Ⅰ)请用列表法(或画树状图法)列出所有可能的结果;
(Ⅱ)求两次取出的小球标号相同的概率;
(Ⅲ)求两次取出的小球标号的和大于6的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
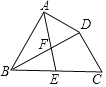
【题目】如图,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F.若BC=4,∠CBD=30°,则DF的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+2kx﹣k2+k+3(k为常数)的顶点纵坐标为4.
(1)求k的值;
(2)设抛物线与直线y=﹣![]() (x﹣3)(m≠0)两交点的横坐标为x1,x2,n=x1+x2﹣2,若A(1,a),B(b,
(x﹣3)(m≠0)两交点的横坐标为x1,x2,n=x1+x2﹣2,若A(1,a),B(b,![]() )两点在动点M(m,n)所形成的曲线上,求直线AB的解析式;
)两点在动点M(m,n)所形成的曲线上,求直线AB的解析式;
(3)将(2)中的直线AB绕点(3,0)顺时针旋转45°,与抛物线x轴上方的部分相交于点C,请直接写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
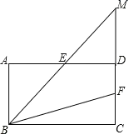
【题目】如图,在四边形ABCD中,AB∥CD,AB=CD,∠A=∠ADC,E,F分别为AD,CD的中点,连接BE,BF,延长BE交CD的延长线于点M.
(1)求证:四边形ABCD为矩形;
(2)若MD=6,BC=12,求BF的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com