
【题目】已知圆O的直径为4cm,A是圆上一固定点,弦BC的长为2![]() cm,当△ABC为等腰三角形时,其底边上的高为_____.
cm,当△ABC为等腰三角形时,其底边上的高为_____.
【答案】![]() 或2,或
或2,或![]()
【解析】
当BC为底边时,如图1,连接AO延长与BC交于F,由全等三角形的判定定理得△ABO≌△ACO,∠BAO=∠CAO,得△ABF≌△ACF,由全等的性质得,BF=CF,由垂径定理得,AF⊥BC,AF为△ABC的高,利用勾股定理可得OF,可得AF的长;
当BC为腰时,如图2,连接BO并延长与AC交于F,由全等三角形的判定定理得△ABO≌△CBO,∠ABO=∠CBO,得△ABF≌△CBF,由全等的性质得,AF=CF,由垂径定理得,BF⊥AC,BF为△ABC的高,由勾股定理逆定理得,△BOC为等腰直角三角形,∠CBO=45°,由等腰三角形的性质得,BF=CF,利用勾股定理可得BF的长;
当如图3所示时,BC为底,利用垂径定理得BF=CF=![]() ,利用勾股定理可得AF的长.
,利用勾股定理可得AF的长.
解:当BC为底边时,如图1,连接AO延长与BC交于F,
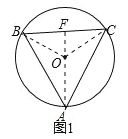
在△ABO与△ACO中,
∴△ABO≌△ACO(SSS),
∴∠BAO=∠CAO,
在△ABF与△ACF中,
∴△ABF≌△ACF(SAS),
∴BF=CF=![]() ,
,
∴AF⊥BC,
∴AF为△ABC的高,
在直角△BOF中,
OF=![]() =
=![]() =
=![]() ,
,
∴AF=2+![]() ;
;
当BC为腰时,如图2,连接BO并延长与AC交于F,
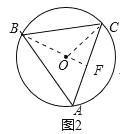
同理可证得:△ABO≌△CBO,
∴∠ABO=∠CBO,
可得△ABF≌△CBF,
∴AF=CF,
∴BF⊥AC,BF为△ABC的高,
∵OB2+OC2=8,BC2=8,
∴△BOC为等腰直角三角形,
∴∠CBO=45°,
∴CF=BF,
设CF=BF=x,
则2x2=8,
解得:x=2,
∴BF=2,
当如图3所示时,BC为底,

∵AF⊥BC,
∴BF=CF=![]() ,
,
设AF=x,则OF=2﹣x,
∴(2﹣x)2+(![]() )2=22,
)2=22,
解得:x=2+![]() 或x=2-
或x=2-![]()
故答案为:2+![]() 或2或2-
或2或2-![]() .
.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,AM是中线,D是AM所在直线上的一个动点(不与点A重合),DE∥AB交AC所在直线于点F,CE∥AM,连接BD,AE.

(1)如图1,当点D与点M重合时,观察发现:△ABM向右平移![]() BC到了△EDC的位置,此时四边形ABDE是平行四边形.请你给予验证;
BC到了△EDC的位置,此时四边形ABDE是平行四边形.请你给予验证;
(2)如图2,图3,图4,是当点D不与点M重合时的三种情况,你认为△ABM应该平移到什么位置?直接在图中画出来.此时四边形ABDE还是平行四边形吗?请你选择其中一种情况说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
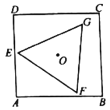
【题目】如图,正方形![]() 的边长为4,在这个正方形内作等边三角形
的边长为4,在这个正方形内作等边三角形![]() (三角形的顶点可以在正方形的边上),使它们的中心重合,则
(三角形的顶点可以在正方形的边上),使它们的中心重合,则![]() 的顶点到正方形
的顶点到正方形![]() 的顶点的最短距离是___________.
的顶点的最短距离是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子里有若干个小球,它们除了颜色外,其它都相同,甲同学从袋子里随机摸出一个球,记下颜色后放回袋子里,摇匀后再次随机摸出一个球,记下颜色,…,甲同学反复大量实验后,根据白球出现的频率绘制了如图所示的统计图,则下列说法正确的是( )
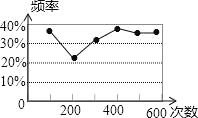
A. 袋子一定有三个白球
B. 袋子中白球占小球总数的十分之三
C. 再摸三次球,一定有一次是白球
D. 再摸1000次,摸出白球的次数会接近330次
查看答案和解析>>
科目:初中数学 来源: 题型:
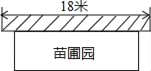
【题目】实验中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长度为30米的篱笆围成已知墙长18米,设这个苗圃园垂直于墙的一边为x米.
(1)若平行于墙的一边的长为y米,直接写出y与x之间的函数关系,以及其自变量的取值范围.
(2)若垂直于墙的一边的长不小于8米,当x为多少米时,这个苗圃的面积最大?求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
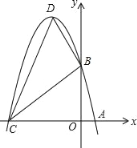
【题目】已知:m,n是方程x2﹣6x+5=0的两个实数根,且m<n,抛物线y=﹣x2+bx+c的图象经过点A(m,0),B(0,n).
(1)求这个抛物线的解析式;
(2)设(1)中的抛物线与x轴的另一交点为C,抛物线的顶点为D,试求出点C,D的坐标和△BCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 和
和![]() ,以下说法:
,以下说法:
①它们的图象都是开口向上;②它们的对称轴都是y轴,顶点坐标都是原点(0,0);③当x>0时,它们的函数y都是随x的增大而增大;④它们的开口的大小是一样的.
其中正确的说法有_______个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com