
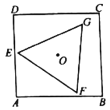
【题目】如图,正方形![]() 的边长为4,在这个正方形内作等边三角形
的边长为4,在这个正方形内作等边三角形![]() (三角形的顶点可以在正方形的边上),使它们的中心重合,则
(三角形的顶点可以在正方形的边上),使它们的中心重合,则![]() 的顶点到正方形
的顶点到正方形![]() 的顶点的最短距离是___________.
的顶点的最短距离是___________.
【答案】![]()
【解析】
当G,O,C共线时,△EFG的顶点到正方形ABCD的顶点的最短,即点G在对角线上,在△AOE中,∠CAE=45°,∠AOE=60°,OE=r,解三角形可求r,即可求最短距离.
如图:当G,O,C共线时,△EFG的顶点到正方形ABCD的顶点的最短,即点G在对角线上.
作EM⊥AC于M
∵ABCD是正方形,AB=4
∴AC=![]() ,AO=
,AO=![]() ,∠CAB=45°
,∠CAB=45°
∵△EFG是等边三角形
∴∠GOE=120°
∴∠AOE=60°
设OE为r
∵∠AOE=60°,ME⊥AO
∴MO=![]() OE=
OE=![]() r,ME=
r,ME=![]() MO=
MO=![]() r
r
∵∠MAE=45°,AM⊥ME
∴∠MAE=∠MEA=45°,
∴AM=ME=![]() r,
r,
∵AM+MO=AO
∴![]() r+
r+![]() r=
r=![]()
∴r=![]()
∵AG=AM=MO+OG=![]() r+
r+![]() r+r=
r+r=![]()
∴GC=![]()
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】函数y=ax2+bx+c的图像如图所示,那么关于x的方程ax2+bx+c-4=0的根的情况是( )

A.有两个不相等的实数根 B.有两个异号的实数根
C.有两个相等的实数根 D.没有实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.
A.如图,DE为△ABC的中位线,点F为DE上一点,且∠AFB=90°,若AB=8,BC=10,则EF的长为________.
B.小智同学在距大雁塔塔底水平距离为138米处,看塔顶的仰角为24.8(不考虑身高因素),则大雁塔市约为________米.(结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
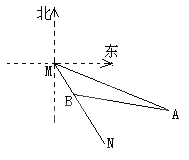
【题目】如图所示,MN表示某饮水工程的一段设计路线,从M到N的走向为南偏东30°,在M的南偏东60°的方向上有一点A,以点A为圆心.以500m为半径的圆形区域为居民区,取MN上另一点B,测得BA的方向为南偏东75°,已知MB=400m.通过计算回答,如果不改变方向,输水路线是否会穿过该居民区?(![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料,并解决相应问题:
材料一:换元法是数学中的重要方法,利用换元法可以从形式上简化式子,在求解某些特殊方程时,利用换元法常常可以达到转化的目的,例如在求解一元四次方程![]() ,就可以令
,就可以令![]() ,则原方程就被换元成
,则原方程就被换元成![]() ,解得 t 1,即
,解得 t 1,即![]() ,从而得到原方程的解是 x 1
,从而得到原方程的解是 x 1
材料二:杨辉三角形是中国数学上一个伟大成就,在中国南宋数学家杨辉 1261 年所著的《详解九章算法》一书中出现,它呈现了某些特定系数在三角形中的一种有规律的几何排列,下图为杨辉三角形:

……………………………………
(1)利用换元法解方程:![]()
(2)在杨辉三角形中,按照自上而下、从左往右的顺序观察, an 表示第 n 行第 2 个数(其中 n≥4),bn 表示第 n 行第 3 个数,![]() 表示第
表示第![]() 行第 3 个数,请用换元法因式分解:
行第 3 个数,请用换元法因式分解:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC 的三个顶点的坐标分别 A(-3,4)B(-5,2)C(-2,1)
(1)画出 △ABC关于y 轴的对称图形 △A1B1C1;
(2)画出将△ABC 绕原点 O逆时针方向旋转90°得到的△A2B2C2 ;
(3)求(2)中线段 OA扫过的图形面积.
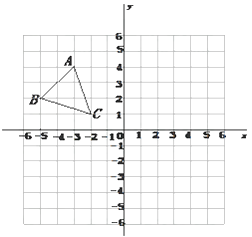
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在倡导“社会主义核心价值观”演讲比赛中,某校根据初赛成绩在七、八年级分别选出10名同学参加决赛,对这些同学的决赛成绩进行整理分析,绘制成如下团体成绩统计表和选手成绩折线统计图:
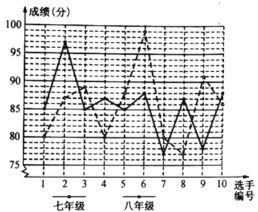
七年级 | 八年级 | |
平均数 | 85.7 | _______ |
众数 | _______ | _______ |
方差 | 37.4 | 27.8 |
根据上述图表提供的信息,解答下列问题:
(1)请你把上面的表格填写完整;
(2)考虑平均数与方差,你认为哪个年级的团体成绩更好?
(3)假设在每个年级的决赛选手中分别选出2个参加决赛,你认为哪个年级的实力更强一些?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com