
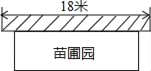
【题目】实验中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长度为30米的篱笆围成已知墙长18米,设这个苗圃园垂直于墙的一边为x米.
(1)若平行于墙的一边的长为y米,直接写出y与x之间的函数关系,以及其自变量的取值范围.
(2)若垂直于墙的一边的长不小于8米,当x为多少米时,这个苗圃的面积最大?求出这个最大值.
【答案】(1)y=30﹣2x(6≤x<15) (2)8 112
【解析】
(1)根据题意即可求得y与x的函数关系式为y=30-2x与自变量x的取值范围为6≤x<15;
(2)设矩形苗圃园的面积为S,由S=xy,即可求得S与x的函数关系式,根据二次函数的最值问题,即可求得这个苗圃园的面积最大值.
解:(1)y=30﹣2x,(6≤x<15);
(2)设矩形苗圃的面积为S,
S=xy=x(30﹣2x)=﹣2(x﹣7.5)2+112.5,
∵垂直于墙的一边的长不小于8米,
∴8≤x<15,
∴当x=8时,S有最大值112,
即当垂直于墙的一边的长为8米时,这个苗圃园的面积最大,这个最大值为112平方米.
故答案为:(1)y=30﹣2x(6≤x<15);(2)8,112.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
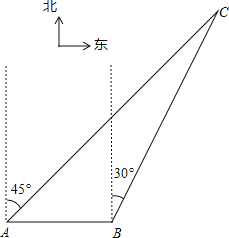
【题目】如图,我渔政310船在南海海面上沿正东方向匀速航行,在A地观测到我渔船C在东北方向上的我国某传统渔场.若渔政310船航向不变,航行半小时后到达B处,此时观测到我渔船C在北偏东30°方向上.问渔政310船再航行多久,离我渔船C的距离最近?(假设我渔船C捕鱼时移动距离忽略不计,结果不取近似值.)
查看答案和解析>>
科目:初中数学 来源: 题型:
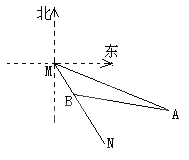
【题目】如图所示,MN表示某饮水工程的一段设计路线,从M到N的走向为南偏东30°,在M的南偏东60°的方向上有一点A,以点A为圆心.以500m为半径的圆形区域为居民区,取MN上另一点B,测得BA的方向为南偏东75°,已知MB=400m.通过计算回答,如果不改变方向,输水路线是否会穿过该居民区?(![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
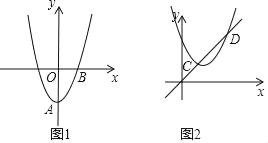
【题目】如图1,在平面直角坐标系中,抛物线C1:y=ax2+bx﹣a2关于y轴对称且有最小值﹣1.
(1)求抛物线C1的解析式;
(2)在图1中抛物线C1顶点为A,将抛物线C1绕 点B旋转180°后得到抛物线C2,直线y=kx﹣2k+4总经过一定点M,若过定点M的直线与抛物线C2只有一个公共点,求直线l的解析式.
(3)如图2,先将抛物线 C1向上平移使其顶点在原点O,再将其顶点沿直线y=x平移得到抛物线C3,设抛物线C3与直线y=x交于C、D两点,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
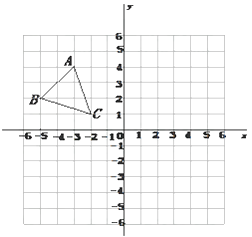
【题目】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC 的三个顶点的坐标分别 A(-3,4)B(-5,2)C(-2,1)
(1)画出 △ABC关于y 轴的对称图形 △A1B1C1;
(2)画出将△ABC 绕原点 O逆时针方向旋转90°得到的△A2B2C2 ;
(3)求(2)中线段 OA扫过的图形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
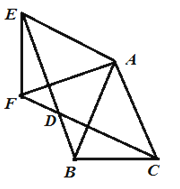
【题目】如图△ABC,AB=AC,将△ABC绕点A顺时针旋转得到△AEF,连结BE、CF相交于点D.
(1)求证:BE=CF;
(2)已知四边形ACDE是菱形,∠BAC=45°,AB=AC=1.
①求旋转角 ∠BAE的度数;
②求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒中有4个完全相同的小球,把它们分别标号为1,2,3,4,随机摸取一个小球然后放回,再随机摸出一个小球.
(Ⅰ)请用列表法(或画树状图法)列出所有可能的结果;
(Ⅱ)求两次取出的小球标号相同的概率;
(Ⅲ)求两次取出的小球标号的和大于6的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com