
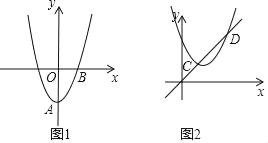
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпC1ЃКy=ax2+bxЉa2ЙигкyжсЖдГЦЧвгазюаЁжЕЉ1ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпC1ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкЭМ1жаХзЮяЯпC1ЖЅЕуЮЊAЃЌНЋХзЮяЯпC1ШЦ ЕуBа§зЊ180ЁуКѓЕУЕНХзЮяЯпC2ЃЌжБЯпy=kxЉ2k+4змОЙ§вЛЖЈЕуMЃЌШєЙ§ЖЈЕуMЕФжБЯпгыХзЮяЯпC2жЛгавЛИіЙЋЙВЕуЃЌЧѓжБЯпlЕФНтЮіЪНЃЎ
ЃЈ3ЃЉШчЭМ2ЃЌЯШНЋХзЮяЯп C1ЯђЩЯЦНвЦЪЙЦфЖЅЕудкдЕуOЃЌдйНЋЦфЖЅЕубижБЯпy=xЦНвЦЕУЕНХзЮяЯпC3ЃЌЩшХзЮяЯпC3гыжБЯпy=xНЛгкCЁЂDСНЕуЃЌЧѓЯпЖЮCDЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=x2Љ1ЃЈ2ЃЉЙ§ЖЈЕуMЃЌЙВгаШ§ЬѕжБЯпlЃКx=2 Лђy=2![]() x+4Љ4
x+4Љ4![]() Лђy=Љ2
Лђy=Љ2![]() x+4+4
x+4+4![]() ЃЌЫќУЧЗжБ№гыХзЮяЯпC3жЛгавЛИіЙЋЙВЕуЃЈ3ЃЉ
ЃЌЫќУЧЗжБ№гыХзЮяЯпC3жЛгавЛИіЙЋЙВЕуЃЈ3ЃЉ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃК ![]() ИљОнХзЮяЯпЕФЖдГЦжсЮЊ
ИљОнХзЮяЯпЕФЖдГЦжсЮЊ![]() жсЃЌЧѓЕУ
жсЃЌЧѓЕУ![]() ХзЮяЯпгазюаЁжЕЃЌПЩЧѓЕУ
ХзЮяЯпгазюаЁжЕЃЌПЩЧѓЕУ![]() ЃЌМДПЩЧѓГіХзЮяЯп
ЃЌМДПЩЧѓГіХзЮяЯп![]() ЕФНтЮіЪН.
ЕФНтЮіЪН.
![]() вРЬтвтПЩЧѓГіХзЮяЯп
вРЬтвтПЩЧѓГіХзЮяЯп![]() ЕФНтЮіЪНЮЊЃК
ЕФНтЮіЪНЮЊЃК ![]() гЩжБЯп
гЩжБЯп![]() змОЙ§вЛЖЈЕуMЃЌПЩЧѓЕУЖЈЕуMЮЊ
змОЙ§вЛЖЈЕуMЃЌПЩЧѓЕУЖЈЕуMЮЊ![]() ЃЌЂйОЙ§ЖЈЕу
ЃЌЂйОЙ§ЖЈЕу![]() гы
гы![]() жсЦНааЕФжБЯп
жсЦНааЕФжБЯп![]() ЃК
ЃК ![]() гыХзЮяЯп
гыХзЮяЯп![]() змгавЛИіЙЋЙВЕу
змгавЛИіЙЋЙВЕу![]() ЃЎЂкОЙ§ЖЈЕу
ЃЎЂкОЙ§ЖЈЕу![]() ЕФжБЯп
ЕФжБЯп![]() ЮЊвЛДЮКЏЪ§
ЮЊвЛДЮКЏЪ§![]() ЪБЃЌгы
ЪБЃЌгы![]() СЊСЂЗНГЬзщЃЌРћгУ
СЊСЂЗНГЬзщЃЌРћгУ![]() ПЩЕУЕУ
ПЩЕУЕУ![]() ЕФжЕЃЌМДПЩЕУГі
ЕФжЕЃЌМДПЩЕУГі![]() Лђ
Лђ![]() ЃЌзлЩЯЫљЪіЃЌЙ§ЖЈЕуMЃЌЙВгаШ§ЬѕжБЯпЫќУЧЗжБ№гыХзЮяЯп
ЃЌзлЩЯЫљЪіЃЌЙ§ЖЈЕуMЃЌЙВгаШ§ЬѕжБЯпЫќУЧЗжБ№гыХзЮяЯп![]() жЛгавЛИіЙЋЙВЕуЃЎ
жЛгавЛИіЙЋЙВЕуЃЎ
![]() ЩшХзЮяЯп
ЩшХзЮяЯп![]() ЕФЖЅЕуЮЊ
ЕФЖЅЕуЮЊ![]() ЃЌвРЬтвтПЩЕУХзЮяЯп
ЃЌвРЬтвтПЩЕУХзЮяЯп![]() ЕФНтЮіЪНЮЊЃК
ЕФНтЮіЪНЮЊЃК ![]() гыжБЯп
гыжБЯп![]() СЊСЂЃЌПЩЕУ
СЊСЂЃЌПЩЕУ![]() ЕФзјБъЃЌЙ§ЕуCзї
ЕФзјБъЃЌЙ§ЕуCзї![]() ЁЮ
ЁЮ![]() жсЃЌЙ§ЕуDзїDMЁЮyжсЃЌПЩЧѓГі
жсЃЌЙ§ЕуDзїDMЁЮyжсЃЌПЩЧѓГі![]() МДПЩЕУГі
МДПЩЕУГі![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉ![]() ХзЮяЯпЕФЖдГЦжсЮЊ
ХзЮяЯпЕФЖдГЦжсЮЊ![]() жсЃЌ
жсЃЌ
![]() НтЕУ
НтЕУ![]()
![]() ХзЮяЯпЕФНтЮіЪНЮЊ
ХзЮяЯпЕФНтЮіЪНЮЊ![]()
![]() ЕБ
ЕБ![]() ХзЮяЯпгазюаЁжЕЃЌМД
ХзЮяЯпгазюаЁжЕЃЌМД![]() НтЕУЃК
НтЕУЃК ![]() Лђ
Лђ![]() ЃЈЩсШЅЃЉЃЎ
ЃЈЩсШЅЃЉЃЎ
ХзЮяЯп![]() ЕФНтЮіЪН
ЕФНтЮіЪН![]()
ЃЈ2ЃЉХзЮяЯп![]() ЕФНтЮіЪН
ЕФНтЮіЪН![]()
![]()
ЩшХзЮяЯп![]() гыxжсЕФСювЛИіНЛЕуЮЊ
гыxжсЕФСювЛИіНЛЕуЮЊ![]() ЃЎ
ЃЎ
Сю![]() ЕУЃК
ЕУЃК ![]() НтЕУЃК
НтЕУЃК ![]()
![]()
НЋХзЮяЯп![]() ШЦЕу
ШЦЕу![]() а§зЊ
а§зЊ![]() КѓЕУЕНХзЮяЯп
КѓЕУЕНХзЮяЯп![]() ЃЌ
ЃЌ
ЁрЕу![]() ЖдгІЕуЕФзјБъЮЊ
ЖдгІЕуЕФзјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЖдгІЕуЕФзјБъЮЊ
ЖдгІЕуЕФзјБъЮЊ![]() .
.
Щш![]() ЕФНтЮіЪНЮЊ
ЕФНтЮіЪНЮЊ![]() НЋ
НЋ![]() ДњШыЕУЃК
ДњШыЕУЃК ![]() НтЕУ
НтЕУ![]()
![]() ЕФНтЮіЪНЮЊ
ЕФНтЮіЪНЮЊ![]()
жБЯп![]() змОЙ§вЛЖЈЕуMЃЌ
змОЙ§вЛЖЈЕуMЃЌ
ЁрЖЈЕуMЮЊ![]() ЃЌ
ЃЌ
ЂйОЙ§ЖЈЕу![]() гы
гы![]() жсЦНааЕФжБЯп
жсЦНааЕФжБЯп![]() ЃК
ЃК ![]() гыХзЮяЯп
гыХзЮяЯп![]() змгавЛИіЙЋЙВЕу
змгавЛИіЙЋЙВЕу![]() ЃЎ
ЃЎ
ЂкНЋ![]() гы
гы![]() СЊСЂЕУЃК
СЊСЂЕУЃК ![]() ећРэЕУЃК
ећРэЕУЃК ![]()
ЁпЙ§ЖЈЕуMЕФжБЯпгыХзЮяЯп![]() жЛгавЛИіЙЋЙВЕуЃЌ
жЛгавЛИіЙЋЙВЕуЃЌ
![]() НтЕУ
НтЕУ![]()
ЁрЙ§ЖЈЕуMЕФжБЯпЕФНтЮіЪНЮЊ![]() Лђ
Лђ![]() ЃЌ
ЃЌ
злЩЯЫљЪіЃЌЙ§ЖЈЕуMЃЌЙВгаШ§ЬѕжБЯпlЃК ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЌЫќУЧЗжБ№гыХзЮяЯп
ЃЌЫќУЧЗжБ№гыХзЮяЯп![]() жЛгавЛИіЙЋЙВЕуЃЎ
жЛгавЛИіЙЋЙВЕуЃЎ
ЃЈ3ЃЉвдЦНвЦКѓХзЮяЯпЕФЖЅЕуЮЊзјБъдЕуНЈСЂзјБъЯЕЃЌдђжБЯпКЭХзЮяЯпдкаТзјБъЯЕЕФНтЮіЪНЮЊ![]() гы
гы![]()
НЋ![]() гы
гы![]() СЊСЂЃЌНтЕУЃК
СЊСЂЃЌНтЕУЃК ![]() Лђ
Лђ![]()
ЁрЕу![]() КЭЕу
КЭЕу![]() дкаТзјБъЯЕФкЕФзјБъЗжБ№ЮЊ
дкаТзјБъЯЕФкЕФзјБъЗжБ№ЮЊ![]()
![]()


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
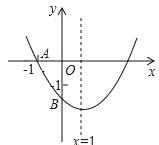
ЁОЬтФПЁПШчЭМЃЌвбжЊЖўДЮКЏЪ§y=ax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓгыxжсНЛгкЕуAЃЈЉ1ЃЌ0ЃЉЃЌгыyжсЕФНЛЕуBдкЃЈ0ЃЌЉ2ЃЉКЭЃЈ0ЃЌЉ1ЃЉжЎМфЃЈВЛАќРЈетСНЕуЃЉЃЌЖдГЦжсЮЊжБЯпx=1ЃЌЃЈ1ЃЉabcЃО0ЃЛЃЈ2ЃЉ4a+2b+cЃО0ЃЛЃЈ3ЃЉ4acЉb2ЃМ16aЃЛЃЈ4ЃЉ![]() ЃМaЃМ
ЃМaЃМ![]() ЃЛЃЈ5ЃЉbЃМcЃЌЦфжае§ШЗЕФНсТлгаЃЈЁЁЁЁЃЉ
ЃЛЃЈ5ЃЉbЃМcЃЌЦфжае§ШЗЕФНсТлгаЃЈЁЁЁЁЃЉ
A. ЃЈ2ЃЉЃЈ3ЃЉЃЈ4ЃЉЃЈ5ЃЉ B. ЃЈ1ЃЉЃЈ3ЃЉЃЈ4ЃЉЃЈ5ЃЉ C. ЃЈ1ЃЉЃЈ3ЃЉЃЈ4ЃЉ D. ЃЈ1ЃЉЃЈ2ЃЉЃЈ5ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
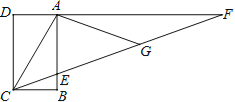
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDжаЃЌAD=![]() ЃЌFЪЧDAбгГЄЯпЩЯвЛЕуЃЌGЪЧCFЩЯвЛЕуЃЌЧвЁЯACG=ЁЯAGCЃЌЁЯGAF=ЁЯF=20ЁуЃЌдђAB=ЁЁЁЁЃЎ
ЃЌFЪЧDAбгГЄЯпЩЯвЛЕуЃЌGЪЧCFЩЯвЛЕуЃЌЧвЁЯACG=ЁЯAGCЃЌЁЯGAF=ЁЯF=20ЁуЃЌдђAB=ЁЁЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпABгыCDЯрНЛгкЕуOЃЌOPЪЧЁЯBOCЕФЦНЗжЯпЃЌOEЁЭABЃЌOFЁЭCDЃЎ
ЃЈ1ЃЉЭМжаГ§жБНЧЭтЃЌЛЙгаЯрЕШЕФНЧТ№ЃПЧыаДГіСНЖдЃЛ
ЃЈ2ЃЉШчЙћЁЯAOD=50ЁуЃЌЧѓЁЯDOPЕФЖШЪ§ЃЎ
ЃЈ3ЃЉOPЦНЗжЁЯEOFТ№ЃПЮЊЪВУДЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП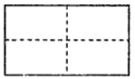
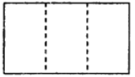
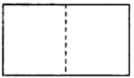
аЁУїЭЈЙ§ЪдбщЗЂЯжЃЛНЋвЛИіОиаЮПЩвдЗжБ№ГЩЫФИіШЋЕШЕФОиаЮЃЌШ§ИіШЋЕШЕФОиаЮЃЌЖўИіШЋЕШЕФОиаЮЃЈШчЩЯЭМЃЉЃЌгкЪЧЫћЖдКЌ![]() ЕФжБНЧШ§НЧаЮНјааЗжБ№баОПЃЌЗЂЯжПЩвдЗжИюГЩЫФИіШЋЕШЕФШ§НЧаЮЃЌШ§ИіШЋЕШЕФШ§НЧаЮ.
ЕФжБНЧШ§НЧаЮНјааЗжБ№баОПЃЌЗЂЯжПЩвдЗжИюГЩЫФИіШЋЕШЕФШ§НЧаЮЃЌШ§ИіШЋЕШЕФШ§НЧаЮ.
ЃЈ1ЃЉЧыФудкЭМ1ЃЌЭМ2вРДЮЛГіЗжИюЯпЃЌВЂМђвЊЫЕУїЛЗЈЃЛ
ЃЈ2ЃЉаЁУїМЬајЯыЗжИюГЩСНИіШЋЕШЕФШ§НЧаЮЃЌЗЂЯжБШНЯРЇФб.ФуФмАбетИіжБНЧШ§НЧаЮЗжИюГЩСНИіШЋЕШЕФШ§НЧаЮТ№ЃПШєФмЃЌЛГіЗжИюЯпЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎЃЈзЂЃКБИгУЭМВЛЙЛгУПЩвдСэЭтЛЃЉ
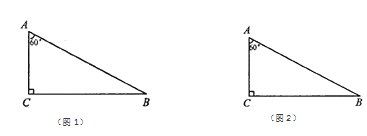
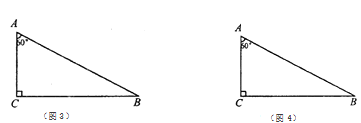
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABCDЕФжмГЄЮЊ36ЃЌЖдНЧЯпACЁЂBDЯрНЛгкЕуOЃЌЕуEЪЧCDЕФжаЕуЃЌBD=12ЃЌдђЁїDOEЕФжмГЄЮЊЃЈЁЁЁЁЃЉ

A. 15 B. 18 C. 21 D. 24
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌEЪЧABБпЕФжаЕуЃЌбиECЖделОиаЮABCDЃЌЪЙBЕуТфдкЕуPДІЃЌелКлЮЊECЃЌСЌНсAPВЂбгГЄAPНЛCDгкFЕуЃЌСЌНсCPВЂбгГЄCPНЛADгкQЕуЃЎИјГівдЯТНсТлЃК
ЂйЫФБпаЮAECFЮЊЦНааЫФБпаЮЃЛ
ЂкЁЯPBA=ЁЯAPQЃЛ
ЂлЁїFPCЮЊЕШбќШ§НЧаЮЃЛ
ЂмЁїAPBЁеЁїEPCЃЎ
Цфжае§ШЗНсТлЕФИіЪ§ЮЊЃЈЁЁЁЁЃЉ
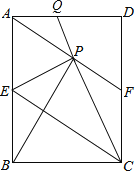
A. 1 B. 2 C. 3 D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуAЃЈ6ЃЌ0ЃЉЃЌBЃЈ8ЃЌ5ЃЉЃЌНЋЯпЖЮOAЦНвЦжСCBЃЌЕуDЃЈxЃЌ0ЃЉдкxжсе§АыжсЩЯЃЈВЛгыЕуAжиКЯЃЉЃЌСЌНгOCЃЌABЃЌCDЃЌBDЃЎ
ЃЈ1ЃЉЧѓЖдНЧЯпACЕФГЄЃЛ
ЃЈ2ЃЉЁїODCгыЁїABDЕФУцЛ§ЗжБ№МЧЮЊS1ЃЌS2ЃЌЩшSЃНS1ЉS2ЃЌЧѓSЙигкxЕФКЏЪ§НтЮіЪНЃЌВЂЬНОПЪЧЗёДцдкЕуDЪЙSгыЁїDBCЕФУцЛ§ЯрЕШЃЌШчЙћДцдкЃЌЧыЧѓГіxЕФжЕЃЈЛђШЁжЕЗЖЮЇЃЉЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
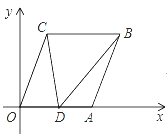
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФвЛдЊЖўДЮЗНГЬ![]() змгаСНИіВЛЯрЕШЕФЪЕЪ§Иљ.
змгаСНИіВЛЯрЕШЕФЪЕЪ§Иљ.
(1)ЧѓmЕФШЁжЕЗЖЮЇЃЛ
(2)ШєДЫЗНГЬЕФСНИљОљЮЊе§ећЪ§ЃЌЧѓе§ећЪ§mЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com