【题目】如图，已知二次函数y=ax2+bx+c（a≠0）的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，﹣2）和（0，﹣1）之间（不包括这两点），对称轴为直线x=1，（1）abc＞0；（2）4a+2b+c＞0；（3）4ac﹣b2＜16a；（4）
＜a＜
；（5）b＜c，其中正确的结论有（ ）
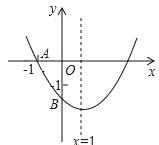
A. （2）（3）（4）（5） B. （1）（3）（4）（5） C. （1）（3）（4） D. （1）（2）（5）
【答案】C
【解析】分析：根据对称轴为直线x=1及图象开口向下可判断出a、b、c的符号，从而判断①；根据对称轴得到函数图象经过（3，0），则得②的判断；根据图象经过（﹣1，0）可得到a、b、c之间的关系，从而对②⑤作判断；从图象与y轴的交点B在（0，﹣2）和（0，﹣1）之间可以判断c的大小得出④的正误．
详解：①∵函数开口方向向上，∴a＞0；
∵对称轴在y轴右侧，∴ab异号．
∵抛物线与y轴交点在y轴负半轴，∴c＜0，∴abc＞0，故①正确；
②∵图象与x轴交于点A（﹣1，0），对称轴为直线x=1，∴图象与x轴的另一个交点为（3，0），∴当x=2时，y＜0，∴4a+2b+c＜0，故②错误；
③∵图象与x轴交于点A（﹣1，0），∴当x=﹣1时，y=（﹣1）2a+b×（﹣1）+c=0，∴a﹣b+c=0，即a=b﹣c，c=b﹣a．
∵对称轴为直线x=1，
∴﹣
=1，即b=﹣2a，∴c=b﹣a=（﹣2a）﹣a=﹣3a，∴4ac﹣b2=4a（﹣3a）﹣（﹣2a）2=﹣16a2＜0．
∵16a＞0，
∴4ac﹣b2＜16a，
故③正确；
④∵图象与y轴的交点B在（0，﹣2）和（0，﹣1）之间，∴﹣2＜c＜﹣1，
∴﹣2＜﹣3a＜﹣1，∴
＜a＜
；
故④正确；
⑤∵a＞0，∴b﹣c＞0，即b＞c；
故⑤错误；
故选C．
科目：初中数学 来源： 题型：
【题目】如图，长方形ABCD中，AB＝3，BC＝4，点E是BC边上任一点，连接AE，把∠B沿AE折叠，使点B落在点B′处，当CE的长为_____时，△CEB′恰好为直角三角形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是一个长方体纸盒的平面展开图，已知纸盒中相对两个面上的数互为相反数．
（1）填空：a＝ ，b＝ ，c＝ ；
（2）先化简，再求值：5a2b﹣[2a2b﹣3（2abc﹣a2b）]+4abc．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料，并解决后面的问题．
材料：对数的创始人是苏格兰数学家纳皮尔（J．Npler，1550-1617年），纳皮尔发明对数是在指数书写方式之前，直到18世纪瑞士数学家欧拉（Evler，1707-1783）才发现指数与对数之间的联系．我们知道，n个相同的因数a相乘
记为
，如
，此时，3叫做以2为底8的对数，记为
，即
．
一般地，若
（
且
，
），则n叫做以a为底b的对数，记为
，即
．如
，则4叫做以3为底81的对数，记为
，即
．
（1）计算下列各对数的值：
________，
________，
________；
（2）通过观察（1）中三数
、
、
之间满足的关系式是________；
（3）拓展延伸；下面这个一般性的结论成立吗？我们来证明
（且
，
，
）
证明：设
，
，
由对数的定义得：
，
，
∴
，
∴
，
又∵
，
，
∴
（且，，）.
（4）仿照（3）的证明，你能证明下面的一般性结论吗？
（且，，）.
（5）计算：
的值为________________.
查看答案和解析>>
科目：初中数学 来源： 题型：
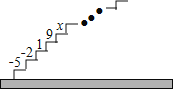
【题目】如图，阶梯图的每个台阶上都标着一个数，从下到上的第1个至第4个台阶上依次标着﹣5，﹣2，1，9，且任意相邻四个台阶上数的和都相等．
尝试 （1）求前4个台阶上数的和是多少？
（2）求第5个台阶上的数x是多少？
应用 求从下到上前31个台阶上数的和．
发现 试用含k（k为正整数）的式子表示出数“1”所在的台阶数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，D，E是△ABC中AB，BC边上的点，且DE∥AC，∠ACB角平分线和它的外角的平分线分别交DE于点G和H．则下列结论错误的是( )
A. 若BG∥CH，则四边形BHCG为矩形
B. 若BE＝CE时，四边形BHCG为矩形
C. 若HE＝CE，则四边形BHCG为平行四边形
D. 若CH＝3，CG＝4，则CE＝2.5
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知函数 y =kx2 +(k +1)x +1（k 为实数），
（1）当 k＝3 时，求此函数图象与 x 轴的交点坐标；
（2）判断此函数与 x 轴的交点个数，并说明理由；
（3）当此函数图象为抛物线，且顶点在 x 轴下方，顶点到 y 轴的距离为 2，求 k 的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）已知y=（m2+m）
+（m﹣3）x+m2是x的二次函数，求出它的解析式．
（2）用配方法求二次函数y=﹣x2+5x﹣7的顶点坐标并求出函数的最大值或最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
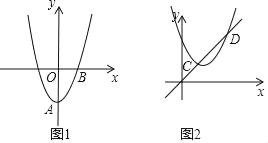
【题目】如图1，在平面直角坐标系中，抛物线C1：y=ax2+bx﹣a2关于y轴对称且有最小值﹣1．
（1）求抛物线C1的解析式；
（2）在图1中抛物线C1顶点为A，将抛物线C1绕 点B旋转180°后得到抛物线C2，直线y=kx﹣2k+4总经过一定点M，若过定点M的直线与抛物线C2只有一个公共点，求直线l的解析式．
（3）如图2，先将抛物线 C1向上平移使其顶点在原点O，再将其顶点沿直线y=x平移得到抛物线C3，设抛物线C3与直线y=x交于C、D两点，求线段CD的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com