
【题目】如图,长方形ABCD中,AB=3,BC=4,点E是BC边上任一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当CE的长为_____时,△CEB′恰好为直角三角形.

【答案】1或![]()
【解析】
分两种情况进行讨论①∠CB′E=90°:∵∠AB′E=∠B=90°,∴B’应在落在直线AC上,设BE=x,根据勾股定理列出方程,求解即可;②∠B′EC=90°,此时ABEB′为正方形,根据正方形的性质计算即可.
解:当△CEB′为直角三角形时,有两种情况:
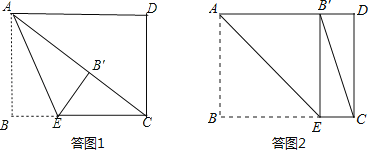
①当点B′落在矩形内部时,如答图1所示.
连结AC,
在Rt△ABC中,AB=3,BC=4,
∴AC=![]() =5,
=5,
∵∠B沿AE折叠,使点B落在点B′处,
∴∠AB′E=∠B=90°,
当△CEB′为直角三角形时,只能得到∠EB′C=90°,
∴点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,
∴EB=EB′,AB=AB′=3,
∴CB′=5﹣3=2,
设BE=x,则EB′=x,CE=4﹣x,
在Rt△CEB′中,
∵EB′2+CB′2=CE2,
∴x2+22=(4﹣x)2,解得x=![]() ,
,
∴BE=![]() ,CE=
,CE=![]()
②当点B′落在AD边上时,如答图2所示.
此时ABEB′为正方形,
∴BE=AB=3,
∴CE=BC﹣BE=4﹣3=1
综上所述:CE=1或![]()
故答案为:1或![]()


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】学校决定从甲、乙两名同学中选拔一人参加“诵读经典”大赛,在相同的测试条件下,甲、乙两人5次测试成绩(单位:分)如下:
甲:79,86,82,85,83.
乙:88,81,85,81,80.
请回答下列问题:
(1)甲成绩的中位数是______,乙成绩的众数是______;
(2)经计算知![]() ,
,![]() .请你求出甲的方差,并从平均数和方差的角度推荐参加比赛的合适人选.
.请你求出甲的方差,并从平均数和方差的角度推荐参加比赛的合适人选.
查看答案和解析>>
科目:初中数学 来源: 题型:
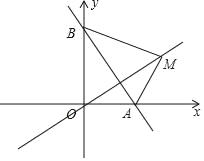
【题目】如图,在平面直角坐标系中,A(p,0),B(0,q),且p、q满足(p﹣2)2+![]() =0.
=0.
(1)求直线AB的解析式;
(2)若点M为直线y=mx上一点,且△ABM是以AB为底的等腰直角三角形,求m值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△ADE都是直角三角形,∠C=∠AED=![]() ,点E在AB上,∠D=
,点E在AB上,∠D=![]() .如果△ABC经顺时针旋转后能与△ADE重合,那么旋转中心是点______,旋转了______度
.如果△ABC经顺时针旋转后能与△ADE重合,那么旋转中心是点______,旋转了______度

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应绿色出行号召,越来越多市民选择租用共享单车出行,已知某共享单车公司为市民提供了手机支付和会员卡支付两种支付方式,如图描述了两种方式应支付金额y(元)与骑行时间x(时)之间的函数关系,根据图象回答下列问题:
(1)求手机支付金额y(元)与骑行时间x(时)的函数关系式;
(2)李老师经常骑行共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[-2.5]=-3;用<a>表示大于a的最小整数,例如:<2.5>=3,<4.5>=5,<-1.5>=-1.解决下列问题.
(1)[-4.5]=_____;<3.5>=________;
(2)若[x]=2,则x的取值范围是________;若<y>=-1,则y的取值范围是_______.
(3)若![]() ,则x为_________.
,则x为_________.
(4)已知x、y满足方程组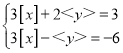
![]() ,求x、y的取值范围.
,求x、y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,AG⊥BG,下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°,其中正确的结论有( )个

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
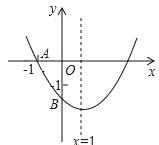
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1,(1)abc>0;(2)4a+2b+c>0;(3)4ac﹣b2<16a;(4)![]() <a<
<a<![]() ;(5)b<c,其中正确的结论有( )
;(5)b<c,其中正确的结论有( )
A. (2)(3)(4)(5) B. (1)(3)(4)(5) C. (1)(3)(4) D. (1)(2)(5)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com