
【题目】如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着﹣5,﹣2,1,9,且任意相邻四个台阶上数的和都相等.
尝试 (1)求前4个台阶上数的和是多少?
(2)求第5个台阶上的数x是多少?
应用 求从下到上前31个台阶上数的和.
发现 试用含k(k为正整数)的式子表示出数“1”所在的台阶数.
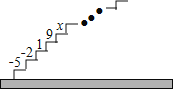
【答案】(1)3;(2)第5个台阶上的数x是﹣5;应用:从下到上前31个台阶上数的和为15;发现:数“1”所在的台阶数为4k﹣1.
【解析】尝试:(1)将前4个数字相加可得;
(2)根据“相邻四个台阶上数的和都相等”列出方程求解可得;
应用:根据“台阶上的数字是每4个一循环”求解可得;
发现:由循环规律即可知“1”所在的台阶数为4k﹣1.
尝试:(1)由题意得前4个台阶上数的和是﹣5﹣2+1+9=3;
(2)由题意得﹣2+1+9+x=3,
解得:x=﹣5,
则第5个台阶上的数x是﹣5;
应用:由题意知台阶上的数字是每4个一循环,
∵31÷4=7…3,
∴7×3+1﹣2﹣5=15,
即从下到上前31个台阶上数的和为15;
发现:数“1”所在的台阶数为4k﹣1.


科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣3x+3与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y= ![]() (k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y=
(k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y= ![]() (k≠0)上的点D1处,则a= .
(k≠0)上的点D1处,则a= . 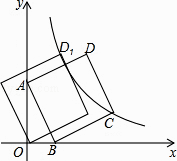
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b在数轴上的表示如图所示,则下列结论中: ①ab<0, ②![]() <0,③a+b<0,④a-b<0,⑤a<|b|,⑥-a>-b,正确的有( )
<0,③a+b<0,④a-b<0,⑤a<|b|,⑥-a>-b,正确的有( )
![]()
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)试验探索:
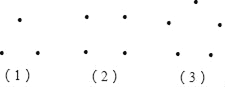
如果过每两点可以画一条直线,那么请下面三组图中分别画线,并回答问题:
第(1)组最多可以画______条直线;
第(2)组最多可以画______条直线;
第(3)组最多可以画______条直线.
(2)归纳结论:
如果平面上有n(n≥3)个点,且每3个点均不在一条直线上,那么最多可以画出直线______条.(作用含n的代数式表示)
(3)解决问题:
某班50名同学在毕业后的一次聚会中,若每两人握一次手问好,则共握 次手;最后,每两个人要互赠礼物留念,则共需 件礼物.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴的正半轴相交,顶点在第四象限,对称轴为x=1,下列结论:①b<0;②a+b<0;③ ![]() <﹣2;④an2+bn=a(2﹣n)2+b(2﹣n)(n为任意实数),其中正确的结论个数是( )
<﹣2;④an2+bn=a(2﹣n)2+b(2﹣n)(n为任意实数),其中正确的结论个数是( ) 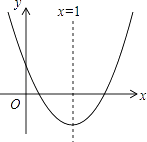
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的四个顶点在坐标轴上,点A的坐标为(﹣3,0),假设有甲,乙两个物体分别由点A同时出发,沿正方形ABCD的边作环绕运动,物体甲按顺时针方向匀速运动,物体乙按逆时针方向匀速运动,若物体甲12秒钟可环绕一周回到点A,物体乙24秒钟可环绕一周回到点A,则两个物体运动后的第2017次相遇地点的坐标是 . 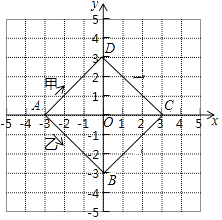
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一平行四边形ABCD与一正方形CEFG,其中E点在AD上.若∠ECD=35°,∠AEF=15°,则∠B的度数为何?( ) 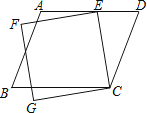
A.50
B.55
C.70
D.75
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com