
【题目】如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点,连结CP并延长CP交AD于Q点.给出以下结论:
①四边形AECF为平行四边形;
②∠PBA=∠APQ;
③△FPC为等腰三角形;
④△APB≌△EPC.
其中正确结论的个数为( )
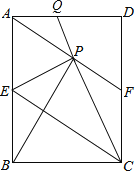
A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】①根据三角形内角和为180°易证∠PAB+∠PBA=90°,易证四边形AECF是平行四边形,即可解题;
②根据平角定义得:∠APQ+∠BPC=90°,由正方形可知每个内角都是直角,再由同角的余角相等,即可解题;
③根据平行线和翻折的性质得:∠FPC=∠PCE=∠BCE,∠FPC≠∠FCP,且∠PFC是钝角,△FPC不一定为等腰三角形;
④当BP=AD或△BPC是等边三角形时,△APB≌△FDA,即可解题.
①如图,EC,BP交于点G;
∵点P是点B关于直线EC的对称点,
∴EC垂直平分BP,
∴EP=EB,
∴∠EBP=∠EPB,
∵点E为AB中点,
∴AE=EB,
∴AE=EP,
∴∠PAB=∠PBA,
∵∠PAB+∠PBA+∠APB=180°,即∠PAB+∠PBA+∠APE+∠BPE=2(∠PAB+∠PBA)=180°,
∴∠PAB+∠PBA=90°,
∴AP⊥BP,
∴AF∥EC;
∵AE∥CF,
∴四边形AECF是平行四边形,
故①正确;
②∵∠APB=90°,
∴∠APQ+∠BPC=90°,
由折叠得:BC=PC,
∴∠BPC=∠PBC,
∵四边形ABCD是正方形,
∴∠ABC=∠ABP+∠PBC=90°,
∴∠ABP=∠APQ,
故②正确;
③∵AF∥EC,
∴∠FPC=∠PCE=∠BCE,
∵∠PFC是钝角,
当△BPC是等边三角形,即∠BCE=30°时,才有∠FPC=∠FCP,
如右图,△PCF不一定是等腰三角形,
故③不正确;
④∵AF=EC,AD=BC=PC,∠ADF=∠EPC=90°,
∴Rt△EPC≌△FDA(HL),
∵∠ADF=∠APB=90°,∠FAD=∠ABP,
当BP=AD或△BPC是等边三角形时,△APB≌△FDA,
∴△APB≌△EPC,
故④不正确;
其中正确结论有①②,2个,
故选:B.


科目:初中数学 来源: 题型:
【题目】已知函数 y =kx2 +(k +1)x +1(k 为实数),
(1)当 k=3 时,求此函数图象与 x 轴的交点坐标;
(2)判断此函数与 x 轴的交点个数,并说明理由;
(3)当此函数图象为抛物线,且顶点在 x 轴下方,顶点到 y 轴的距离为 2,求 k 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列证明:如图,已知AD⊥BC,EF⊥BC,∠1=∠2.
求证: DG∥BA.
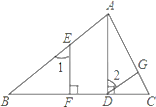
证明:∵AD⊥BC,EF⊥BC ( 已知 )
∴∠EFB=90°,∠ADB=90°(_______________________ )
∴∠EFB=∠ADB ( 等量代换 )
∴EF∥AD ( _________________________________ )
∴∠1=∠BAD (________________________________________)
又∵∠1=∠2 ( 已知)
∴ (等量代换)
∴DG∥BA. (__________________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线C1:y=ax2+bx﹣a2关于y轴对称且有最小值﹣1.
(1)求抛物线C1的解析式;
(2)在图1中抛物线C1顶点为A,将抛物线C1绕 点B旋转180°后得到抛物线C2,直线y=kx﹣2k+4总经过一定点M,若过定点M的直线与抛物线C2只有一个公共点,求直线l的解析式.
(3)如图2,先将抛物线 C1向上平移使其顶点在原点O,再将其顶点沿直线y=x平移得到抛物线C3,设抛物线C3与直线y=x交于C、D两点,求线段CD的长.
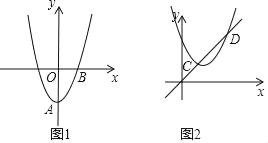
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:

(1)这次统计共抽查了 名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为 ;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
(4)某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选中同一种沟通方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加“荆州市中小学生首届诗词大会”,某校八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(1)班86,85,77,92,85;八(2)班79,85,92,85,89.通过数据分析,列表如下:
班级 | 平均分 | 中位数 | 众数 | 方差 |
八(1) | 85 | b | c | 22.8 |
八(2) | a | 85 | 85 | 19.2 |
(1)直接写出表中a,b,c的值;
(2)根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
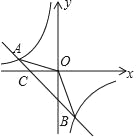
【题目】(8分)已知A(﹣4,m+10)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y=![]() 图象的两个交点.
图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b﹣![]() >0的解集.
>0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防“甲型H1N1”,某校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量低于1.6mg时,生方可进教室,那么从消毒开始,至少需要几分钟后,生才能进入教室?
(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料263千克,乙种原料314千克,计划利用这两种原料生产A、B两种产品共100件.生产一件产品所需要的原料及生产成本如下表所示:
甲种原料(单位:千克) | 乙种原料(单位:千克) | 生产成本(单位:元) | |
A产品 | 3 | 2 | 120 |
B产品 | 2.5 | 3.5 | 200 |
(1)该工厂现有的原料能否保证生产需要?若能,有几种生产方案?请你设计出来.
(2)设生产A、B两种产品的总成本为y元,其中生产A产品x件,试写出y与x之间的函数关系,并利用函数的性质说明(1)中哪种生产方案总成本最低?最低生产总成本是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com