
【题目】已知抛物线y=﹣x2+2kx﹣k2+k+3(k为常数)的顶点纵坐标为4.
(1)求k的值;
(2)设抛物线与直线y=﹣![]() (x﹣3)(m≠0)两交点的横坐标为x1,x2,n=x1+x2﹣2,若A(1,a),B(b,
(x﹣3)(m≠0)两交点的横坐标为x1,x2,n=x1+x2﹣2,若A(1,a),B(b,![]() )两点在动点M(m,n)所形成的曲线上,求直线AB的解析式;
)两点在动点M(m,n)所形成的曲线上,求直线AB的解析式;
(3)将(2)中的直线AB绕点(3,0)顺时针旋转45°,与抛物线x轴上方的部分相交于点C,请直接写出点C的坐标.
【答案】(1)1;(2)![]() ;(3)(2,3).
;(3)(2,3).
【解析】
(1)利用配方法即可解决问题;
(2)由题意,方程-x2+2x+3=-![]() (x-3)的两实数根分别为x1,x2,整理得,
(x-3)的两实数根分别为x1,x2,整理得,![]() ,推出x1+x2=
,推出x1+x2=![]() +2,由n=x1+x2﹣2,推出n=
+2,由n=x1+x2﹣2,推出n=![]() +2-2=
+2-2=![]() ,即动点M(m,n)所形成的曲线为y=
,即动点M(m,n)所形成的曲线为y=![]() ,由A(1,a),B(b,
,由A(1,a),B(b,![]() )两点在该曲线上,推出A(1,1),B(2,
)两点在该曲线上,推出A(1,1),B(2,![]() ),再利用待定系数法即可解决问题;
),再利用待定系数法即可解决问题;
(3)由直线AB的解析式为y=﹣![]() x+
x+![]() ,A(1,1),推出点D(3,0)在直线AB上,取点E(2,3),则AE=AD=
,A(1,1),推出点D(3,0)在直线AB上,取点E(2,3),则AE=AD=![]() ,ED=
,ED=![]() ,推出AE2+AD2=ED2,推出∠EAD=90°,由AE=AD,推出∠ADE=45°,可得直线ED的解析式为y=﹣3x+9,构建方程组即可求出点C坐标.
,推出AE2+AD2=ED2,推出∠EAD=90°,由AE=AD,推出∠ADE=45°,可得直线ED的解析式为y=﹣3x+9,构建方程组即可求出点C坐标.
(1)y=﹣x2+2kx﹣k2+k+3=﹣(x﹣k)2+k+3,
∵顶点纵坐标为4,
∴k+3=4,
∴k=1;
(2)∵k=1,
∴抛物线为y=﹣x2+2x+3,
由题意,方程-x2+2x+3=-![]() (x-3)的两实数根分别为x1,x2,
(x-3)的两实数根分别为x1,x2,
整理得,![]() ,
,
∴x1+x2=![]() +2,
+2,
∵n=x1+x2﹣2,
∴n=![]() +2-2=
+2-2=![]() ,
,
即动点M(m,n)所形成的曲线为y=![]() ,
,
∵A(1,a),B(b,![]() )两点在该曲线上,
)两点在该曲线上,
∴A(1,1),B(2,![]() ),
),
设直线AB解析式为y=k'x+b',把A(1,1),B(2,![]() )代入得,
)代入得,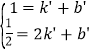 ,
,
解得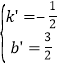 ,
,
∴直线AB的解析式为y=﹣![]() x+
x+![]() ;
;
(3)如图,
∵直线AB的解析式为y=﹣![]() x+
x+![]() ,A(1,1),
,A(1,1),
∴点D(3,0)在直线AB上,
取点E(2,3),则AE=AD=![]() ,ED=
,ED=![]() ,
,
∴AE2+AD2=ED2,
∴∠EAD=90°,
∵AE=AD,
∴∠ADE=45°,
∵设直线DE解析式为y=k″x+b″,把D(3,0),E(2,3)代入得,![]() ,
,
解得![]() ,
,
∴直线ED的解析式为y=﹣3x+9,
由![]() ,解得
,解得![]() 或
或![]() ,
,
∵D(3,0),
∴C(2,3).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】二次函数![]() 和
和![]() ,以下说法:
,以下说法:
①它们的图象都是开口向上;②它们的对称轴都是y轴,顶点坐标都是原点(0,0);③当x>0时,它们的函数y都是随x的增大而增大;④它们的开口的大小是一样的.
其中正确的说法有_______个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店以固定进价一次性购进一种商品,3月份按一定售价销售,销售额为2400元,为扩大销量,减少库存,4月份在3月份售价基础上打9折销售,结果销售量增加30件,销售额增加840元.
(1)求该商店3月份这种商品的售价是多少元?
(2)如果该商店3月份销售这种商品的利润为900元,那么该商店4月份销售这种商品的利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某报社为了解市民对“社会主义核心价值观”的知晓程度,采取随机抽样的方式进行问卷调查,调查结果为“A非常了解”、“B了解”、“C基本了解”三个等级,并根据调查结果制作了如下两幅不完整的统计图.
请根据图中提供的信息,解答下列问题:
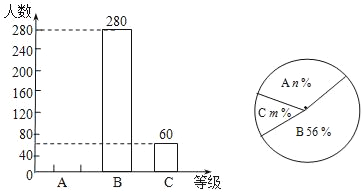
(1)本次调查的人数为 ;
(2)补全条形统计图;
(3)若该市约有市民100万人,请你根据抽样调查的结果,估计该市大约有多少人对“社会主义核心价值观”达到“A非常了解”的程度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,吊车在水平地面上吊起货物时,吊绳BC与地面保持垂直,吊臂AB与水平线的夹角为64°,吊臂底部A距地面1.5m.(计算结果精确到0.1m,参考数据sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)
(1)当吊臂底部A与货物的水平距离AC为5m时,吊臂AB的长为多少m.
(2)如果该吊车吊臂的最大长度AD为20m,那么从地面上吊起货物的最大高度是多少?(吊钩的长度与货物的高度忽略不计)
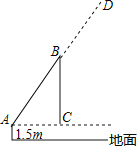
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是( )
A. 30° B. 60° C. 30°或150° D. 60°或120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,将一块正方形纸板OEFG如图1摆放,它的顶点O与矩形ABCD的对角线交点重合,点A在正方形的边OG上,现将正方形绕点O逆时针旋转,当点B在OG边上时,停止旋转,在旋转过程中OG交AB于点M,OE交AD于点N.
(1)开始旋转前,即在图1中,连接NC.
①求证:NC=NA(M);
②若图1中NA(M)=4,DN=2,请求出线段CD的长度.
(2)在图2(点B在OG上)中,请问DN、AN、CD这三条线段之间有什么数量关系?写出结论,并说明理由.
(3)试探究图3中AN、DN、AM、BM这四条线段之间有什么数量关系?写出结论,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3700米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°,求这座山的高度CD.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com