
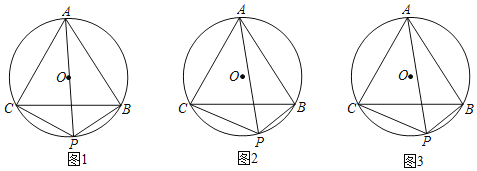
【题目】如图,△ABC是⊙O的内接正三角形,点P在劣弧BC上(不与点B,C重合).
(1)如图1,若PA是⊙O的直径,则PA______PB+PC(请填“>”,“=”或“<”)
(2)如图2,若PA不是⊙O的直径,那么(1)中的结论是否仍成立?如果不成立,请说明理由:如果成立,请给出证明.
(3)如图3,若四边形ACPB的面积是16![]() .
.
①求PA的长;
②设y=S△PCB+![]() S△PCA,求当PC为何值时,y的值最大?并直接写出此时⊙O的半径.
S△PCA,求当PC为何值时,y的值最大?并直接写出此时⊙O的半径.
【答案】(1)=;(2)结论仍然成立,理由见解析.(3)①PA=8,②PC=5,y的值最大,△ABC的外接圆的半径为![]() .
.
【解析】
(1)根据△ABC是等边三角形,⊙O是△ABC的外接圆,PA是直径,得PC=![]() PA,PB=
PA,PB=![]() PA;(2)根据等边三角形的性质和判定,可证△CBE≌△ABE(SAS),PC=AE,故PA=PE+AE=PB+PC;(3)①如图3中,作CM⊥PA于M,BN⊥PA于N.根据S四边形ACPB=S△PAC+S△PAB得16
PA;(2)根据等边三角形的性质和判定,可证△CBE≌△ABE(SAS),PC=AE,故PA=PE+AE=PB+PC;(3)①如图3中,作CM⊥PA于M,BN⊥PA于N.根据S四边形ACPB=S△PAC+S△PAB得16![]() =
=![]() PACM+
PACM+![]() PABN,根据三角函数得CM=PCsin60°,BN=PCsin60°,故16
PABN,根据三角函数得CM=PCsin60°,BN=PCsin60°,故16![]() =
=![]() PA(PB+PC),PA2=64;②设PC=x,则PB=8-x,
PA(PB+PC),PA2=64;②设PC=x,则PB=8-x,
由y=S△PCB+![]() S△PCA=
S△PCA=![]() PCPBsin60°+
PCPBsin60°+![]() 8PCsin60°,得y=
8PCsin60°,得y=![]() x(8-x)+
x(8-x)+![]() x=-
x=-![]() x2+
x2+![]() x=-
x=-![]() (x-5)2+
(x-5)2+![]() ,根据二次函数二次函数最值性质和勾股定理可求解.
,根据二次函数二次函数最值性质和勾股定理可求解.
解:(1)如图1中,
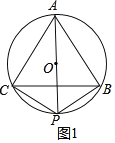
∵△ABC是等边三角形,⊙O是△ABC的外接圆,PA是直径,
∴PA平分∠BAC,∠ACP=∠ABP=90°,
∴∠PAC=∠PAB=![]() ×60°=30°,
×60°=30°,
∴PC=![]() PA,PB=
PA,PB=![]() PA,
PA,
∴PA=PB+PC.
故答案为=.
(2)结论仍然成立.
理由:如图2中,在PA上取一点E,使得PE=PB.
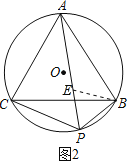
∵△ABC是等边三角形,
∴∠ACB=∠ABC=60°,
∴∠APB=∠ACB=60°,
∵PE=PB,
∴△PBE是等边三角形,
∴∠PBE=∠ABC=60°,
∴∠ABE=∠CBP,
∵BC=BA,BP=BE,
∴△CBE≌△ABE(SAS),
∴PC=AE,
∴PA=PE+AE=PB+PC.
(3)①如图3中,作CM⊥PA于M,BN⊥PA于N.
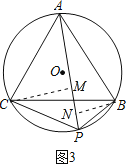
∵S四边形ACPB=S△PAC+S△PAB,
∴16![]() =
=![]() PACM+
PACM+![]() PABN,
PABN,
∵∠APC=∠ABC=60°,∠APB=∠ACB=60°,
∴CM=PCsin60°,BN=PCsin60°,
∴16![]() =
=![]() PA(PB+PC),
PA(PB+PC),
∵PB+PC=PA,
∴PA2=64,
∵PA>0,
∴PA=8.
②设PC=x,则PB=8-x,
∵y=S△PCB+![]() S△PCA=
S△PCA=![]() PCPBsin60°+
PCPBsin60°+![]() 8PCsin60°,
8PCsin60°,
∴y=![]() x(8-x)+
x(8-x)+![]() x=-
x=-![]() x2+
x2+![]() x=-
x=-![]() (x-5)2+
(x-5)2+![]() ,
,
∵-![]() <0,
<0,
∴x=5时,y有最大值,
∴PC=5,CM=![]() ,PM=
,PM=![]() ,AM=
,AM=![]() ,
,
在Rt△ACM中,AC=![]() =7,
=7,
∴△ABC的外接圆的半径为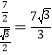 .
.


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-(m+1)x+![]() (m2+1)=0.
(m2+1)=0.
(1)若该方程有实数根,求m的值.
(2)对于函数y1=x2-(m+1)x+![]() (m2+1),当x>1时,y1随着x的增大而增大.
(m2+1),当x>1时,y1随着x的增大而增大.
①求m的范围.
②若函数y2=2x+n与函数![]() 交于y轴上同一点,求n的最小值.
交于y轴上同一点,求n的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知AB是⊙O 的直径,C是⊙O 上一点,∠ACB的平分线交⊙O 于点D,作PD∥AB,交CA的延长线于点P.连结AD,BD.
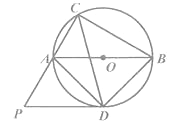
求证:(1)PD是⊙O 的切线;
(2)△PAD![]() △DBC.
△DBC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为推动“时刻听党话 永远跟党走”校园主题教育活动,计划开展四项活动:A:党史演讲比赛,B:党史手抄报比赛,C:党史知识竞赛,D:红色歌咏比赛.校团委对学生最喜欢的一项活动进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2两幅不完整的统计图.请结合图中信息解答下列问题:
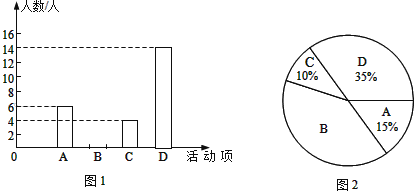
(1)本次共调查了 名学生;
(2)将图1的统计图补充完整;
(3)已知在被调查的最喜欢“党史知识竞赛”项目的4个学生中只有1名女生,现从这4名学生中任意抽取2名学生参加该项目比赛,请用画树状图或列表的方法,求出恰好抽到一名男生一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD和正方形AEFG中,边AE在边AB上,AB=![]() ,AE=1.将正方形AEFG绕点A逆时针旋转,设BE的延长线交直线DG于点P,当点P,G第一次重合时停止旋转.在这个过程中:
,AE=1.将正方形AEFG绕点A逆时针旋转,设BE的延长线交直线DG于点P,当点P,G第一次重合时停止旋转.在这个过程中:
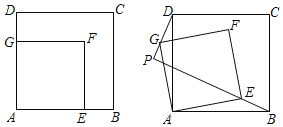
(1)∠BPD=______度;
(2)点P所经过的路径长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
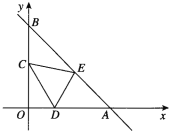
【题目】已知:如图,直线y=-x+12分别交x轴、y轴于A、B点,将△AOB折叠,使A点恰好落在OB的中点C处,折痕为DE.
(1)求AE的长及sin∠BEC的值;
(2)求△CDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示.根据图象所提供的信息有:①甲队挖掘30m时,用了3h;②挖掘6h时甲队比乙队多挖了10m;③乙队的挖掘速度总是小于甲队;④开挖后甲、乙两队所挖河渠长度相等时,x=4.其中一定正确的有( )
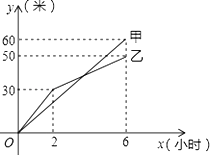
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
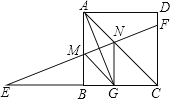
【题目】如图,在正方形ABCD中,∠BAC的平分线交BC边于G,AG的中垂线与CB的延长线交于E,与AB、AC、DC分别交于点M,N,F,下列结论:①tan∠E=![]() ,②△AGC≌△EMG,③四边形AMGN是菱形,④S△CFN=S四边形AMGN,其中正确的是______(填序号).
,②△AGC≌△EMG,③四边形AMGN是菱形,④S△CFN=S四边形AMGN,其中正确的是______(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
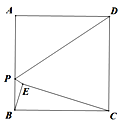
【题目】如图,正方形ABCD的边长为6,点E是正方形内部一点,连接BE,CE,且∠ABE=∠BCE,点P是边AB上一动点,连接PD,PE,则PD+PE的最小值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com