
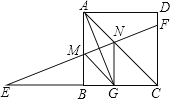
【题目】如图,在正方形ABCD中,∠BAC的平分线交BC边于G,AG的中垂线与CB的延长线交于E,与AB、AC、DC分别交于点M,N,F,下列结论:①tan∠E=![]() ,②△AGC≌△EMG,③四边形AMGN是菱形,④S△CFN=S四边形AMGN,其中正确的是______(填序号).
,②△AGC≌△EMG,③四边形AMGN是菱形,④S△CFN=S四边形AMGN,其中正确的是______(填序号).
【答案】②③④
【解析】
在正方形ABCD中,∠BAC的平分线交BC边于G,可得∠BAG=∠CAG=![]() ∠BAC=22.5°,∠AGB=67.5°,因为AG的中垂线与CB的延长线交于E,可得AM=MG,AN=NG,∠E=22.5°,即可判断①错误,证明AM=AN,可得AM=GM=NG=AN,即四边形AMGN是菱形,可判断③正确;用“角角边”可证明△AGC≌△EMG,可判断②正确;证明意△AMN∽△CFN,可得S△CFN=2S△AMN=S四边形AMGN,可判断④正确.
∠BAC=22.5°,∠AGB=67.5°,因为AG的中垂线与CB的延长线交于E,可得AM=MG,AN=NG,∠E=22.5°,即可判断①错误,证明AM=AN,可得AM=GM=NG=AN,即四边形AMGN是菱形,可判断③正确;用“角角边”可证明△AGC≌△EMG,可判断②正确;证明意△AMN∽△CFN,可得S△CFN=2S△AMN=S四边形AMGN,可判断④正确.
解:∵在正方形ABCD中,∠BAC的平分线交BC边于G,
∴∠BAG=∠CAG=![]() ∠BAC=22.5°,
∠BAC=22.5°,
∵∠ABC=90°,
∴∠AGB=90°-22.5°=67.5°,
∵AG的中垂线与CB的延长线交于E,
∴AM=MG,AN=NG,∠E=90°-∠AGB=22.5°,
∴tan∠E=![]() 错误,即①错误;
错误,即①错误;
∵∠AMN=∠ANM=90°-22.5°=67.5°,
∴AM=AN,
∴AM=GM=NG=AN,
∴四边形AMGN是菱形,即③正确;
∵四边形AMGN是菱形,
∴MG∥AC,AB∥NG,
∴∠ACG=∠MGE=45°,∠NGC=∠ABC=90°,
∴GC=GN=GM,
∵∠GAC=∠E=22.5°,
∴△AGC≌△EMG(AAS),即②正确;
由题意△AMN∽△CFN,
∴![]() ,
,
∴S△CFN=2S△AMN=S四边形AMGN,即④正确.
故答案为:②③④.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:初中数学 来源: 题型:
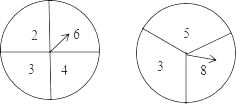
【题目】初三年(4)班要举行一场毕业联欢会,主持人同时转动下图中的两个转盘(每个转盘分别被四等分和三等分),由一名同学在转动前来判断两个转盘上指针所指的两个数字之和是奇数还是偶数,如果判断错误,他就要为大家表演一个节目;如果判断正确,他可以指派别人替自己表演节目.现在轮到小明来选择,小明不想自己表演,于是他选择了偶数.小明的选择合理吗?从概率的角度进行分析(要求用树状图或列表方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
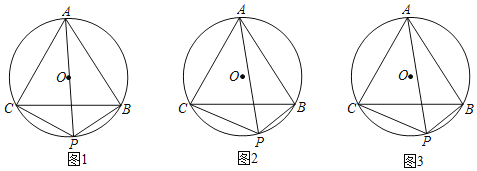
【题目】如图,△ABC是⊙O的内接正三角形,点P在劣弧BC上(不与点B,C重合).
(1)如图1,若PA是⊙O的直径,则PA______PB+PC(请填“>”,“=”或“<”)
(2)如图2,若PA不是⊙O的直径,那么(1)中的结论是否仍成立?如果不成立,请说明理由:如果成立,请给出证明.
(3)如图3,若四边形ACPB的面积是16![]() .
.
①求PA的长;
②设y=S△PCB+![]() S△PCA,求当PC为何值时,y的值最大?并直接写出此时⊙O的半径.
S△PCA,求当PC为何值时,y的值最大?并直接写出此时⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
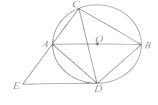
【题目】如图,AB是⊙O的直径,![]() ,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
(1)求∠BAC的度数;
(2)当点D在AB上方,且CD⊥BP时,求证:PC=AC;
(3)在点P的运动过程中
①当点A在线段PB的中垂线上或点B在线段PA的中垂线上时,求出所有满足条件的∠ACD的度数;
②设⊙O的半径为6,点E到直线l的距离为3,连结BD,DE,直接写出△BDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=10,弦AC=6,∠ACB的平分线交⊙O于点D,过点D作DE∥AB交CA延长线于点E,连接AD,BD.
(1)△ABD的面积是________:
(2)求证:DE是⊙O的切线:
(3)求线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)求每套队服和每个足球的价格是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两个全等的直角三角形ABC和DBE按图![]() 方式摆放,其中
方式摆放,其中![]() ,
,![]() ,点E落在AB上,DE所在直线交AC所在直线于点F.
,点E落在AB上,DE所在直线交AC所在直线于点F.
![]() 求证:
求证:![]() ;
;
![]() 若将图
若将图![]() 中的
中的![]() 绕点B按顺时针方向旋转角a,且
绕点B按顺时针方向旋转角a,且![]() ,其他条件不变,如图
,其他条件不变,如图![]() 请你直接写出
请你直接写出![]() 与DE的大小关系:
与DE的大小关系:![]() ______
______![]() 填“
填“![]() ”或“
”或“![]() ”或“
”或“![]() ”
”![]()
![]() 若将图
若将图![]() 中
中![]() 的绕点B按顺时针方向旋转角
的绕点B按顺时针方向旋转角![]() ,且
,且![]() ,其他条件不变,如图
,其他条件不变,如图![]() 请你写出此时AF、EF与DE之间的关系,并加以证明.
请你写出此时AF、EF与DE之间的关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,射线AP交⊙O于C点,∠PCO的平分线交⊙O于D点,过点D作![]() 交AP于E点.
交AP于E点.
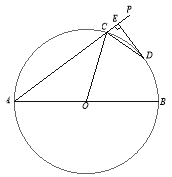
(1)求证:DE为⊙O的切线;
(2)若DE=3,AC=8,求直径AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线![]() 的一部分,如图
的一部分,如图
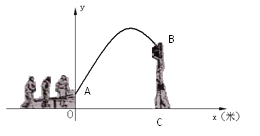
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com