
【题目】将两个全等的直角三角形ABC和DBE按图![]() 方式摆放,其中
方式摆放,其中![]() ,
,![]() ,点E落在AB上,DE所在直线交AC所在直线于点F.
,点E落在AB上,DE所在直线交AC所在直线于点F.
![]() 求证:
求证:![]() ;
;
![]() 若将图
若将图![]() 中的
中的![]() 绕点B按顺时针方向旋转角a,且
绕点B按顺时针方向旋转角a,且![]() ,其他条件不变,如图
,其他条件不变,如图![]() 请你直接写出
请你直接写出![]() 与DE的大小关系:
与DE的大小关系:![]() ______
______![]() 填“
填“![]() ”或“
”或“![]() ”或“
”或“![]() ”
”![]()
![]() 若将图
若将图![]() 中
中![]() 的绕点B按顺时针方向旋转角
的绕点B按顺时针方向旋转角![]() ,且
,且![]() ,其他条件不变,如图
,其他条件不变,如图![]() 请你写出此时AF、EF与DE之间的关系,并加以证明.
请你写出此时AF、EF与DE之间的关系,并加以证明.

【答案】(1)证明见解析;(2)=;(3)AF-EF=DE.
【解析】
试题(1)如图,连接BF,由△ABC≌△DBE,可得BC=BE,根据直角三角形的“HL”定理,易证△BCF≌△BEF,即可证得;
(2)同(1)得CF=EF,由△ABC≌△DBE,可得AC=DE,AC=AF+CF=AF+EF,所以AF+EF=DE;
(3)同(1)得CF=EF,由△ABC≌△DBE,可得AC=DE,AF=AC+FC=DE+EF.
试题解析:
(1)证明:如图(1)连接BF, ∵Rt△ABC≌Rt△DBE,
∴BC=BE,
又BF=BF,
∴Rt△BCF≌Rt△BEF(HL),
∴CF![]() EF.
EF.
(2)=
(3)AF-EF=DE,
证明:如图(3),连接BF,
同(1)证明可知:CF![]() EF,
EF,
又DE![]() AC,
AC,
由图可知AF-CF=AC,
∴AF-EF=DE.
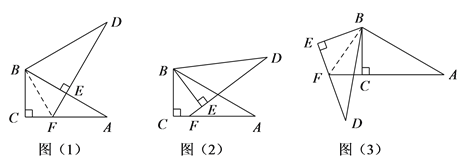


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,己知AB是⊙O 的直径,C是⊙O 上一点,∠ACB的平分线交⊙O 于点D,作PD∥AB,交CA的延长线于点P.连结AD,BD.
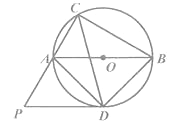
求证:(1)PD是⊙O 的切线;
(2)△PAD![]() △DBC.
△DBC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示.根据图象所提供的信息有:①甲队挖掘30m时,用了3h;②挖掘6h时甲队比乙队多挖了10m;③乙队的挖掘速度总是小于甲队;④开挖后甲、乙两队所挖河渠长度相等时,x=4.其中一定正确的有( )
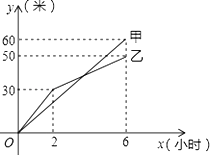
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
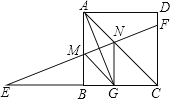
【题目】如图,在正方形ABCD中,∠BAC的平分线交BC边于G,AG的中垂线与CB的延长线交于E,与AB、AC、DC分别交于点M,N,F,下列结论:①tan∠E=![]() ,②△AGC≌△EMG,③四边形AMGN是菱形,④S△CFN=S四边形AMGN,其中正确的是______(填序号).
,②△AGC≌△EMG,③四边形AMGN是菱形,④S△CFN=S四边形AMGN,其中正确的是______(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
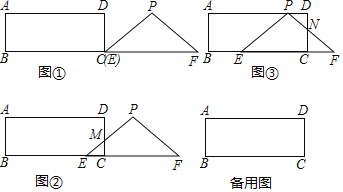
【题目】已知:Rt△EFP和矩形ABCD如图①摆放(点C与点E重合),点B,C(E),F在同一直线上,AB=3cm,BC=9cm,EF=8cm,PE=PF=5cm,如图②,△EFP从图①的位置出发,沿CB方向匀速运动,速度为2cm/s,当点F与点C重合时△EFP停止运动停止.设运动时间为t(s)(0<t<4),解答下列问题:
(1)当0<t<2时,EP与CD交于点M,请用含t的代数式表示CE=______,CM=______;
(2)当2<t<4时,如图③,PF与CD交于点N,设四边形EPNC的面积为y(cm2),求y与t之间的函数关系式;
(3)当2<t<4时,且S四边形EPNC:S矩形ABCD=1:4时,请求出t的值;
(4)连接BD,在运动过程中,当BD与EP相交时,设交点为O,当t=______时;O在∠BAD的平分线上.(不需要写解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
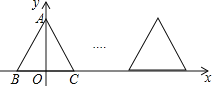
【题目】已知等边三角形ABC在平面直角坐标系中的位置如图所示,C(1,0),点A在y轴的正半轴上,把等边三角形ABC沿x轴正半轴作无滑动的连续翻转,每次翻转120°,经过2018次翻转之后,点C的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
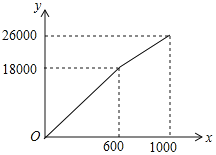
【题目】为了创建“全国文明城市”,鄂州市积极主动建设美丽家园,某社区拟将一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草面积为x(m2),种草费用y1(元)与x(m2)的函数关系式为y1=![]() ,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系如表所示:
,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系如表所示:
x(m2) | 100 | 200 | 300 |
y2(元) | 3900 | 7600 | 11100 |
(1)请直接写出y1与种草面积x(m2)的函数关系式,y2与栽花面积x(m2)的函数关系式;
(2)设这块1000m2空地的绿化总费用为W(元),请利用W与种草面积x(m2)的函数关系式,求出绿化总费用W的最大值;
(3)若种草部分的面积不少于600m2,栽花部分的面积不少于200m2,请求出绿化总费用W的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
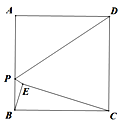
【题目】如图,正方形ABCD的边长为6,点E是正方形内部一点,连接BE,CE,且∠ABE=∠BCE,点P是边AB上一动点,连接PD,PE,则PD+PE的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
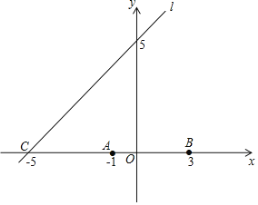
【题目】已知抛物线y=ax2+bx-3的图象与x轴交于点A(-1,0)和点B(3,0),顶点为D,点C是直线l:y=x+5与x轴的交点.
(1)求该二次函数的表达式;
(2)点E是直线l在第三象限上的点,连接EA、EB,当△ECA∽△BCE时,求E点的坐标;
(3)在(2)的条件下,连接AD、BD,在直线DE上是否存在点P,使得∠APD=∠ADB?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com