
【题目】一个不透明袋子中有1个红球和n个白球,这些球除颜色外无其他差别.
(1)从袋中随机摸出一个球,记录其颜色,然后放回.大量重复该实验,发现摸到红球的频率稳定于0.25,求n的值.
(2)在(1)的条件下,从袋中随机摸出两个球,求两个球颜色不同的概率.
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示.根据图象所提供的信息有:①甲队挖掘30m时,用了3h;②挖掘6h时甲队比乙队多挖了10m;③乙队的挖掘速度总是小于甲队;④开挖后甲、乙两队所挖河渠长度相等时,x=4.其中一定正确的有( )
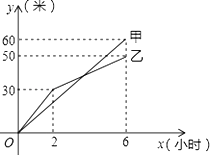
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
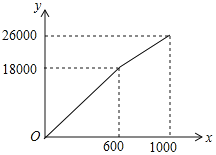
【题目】为了创建“全国文明城市”,鄂州市积极主动建设美丽家园,某社区拟将一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草面积为x(m2),种草费用y1(元)与x(m2)的函数关系式为y1=![]() ,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系如表所示:
,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系如表所示:
x(m2) | 100 | 200 | 300 |
y2(元) | 3900 | 7600 | 11100 |
(1)请直接写出y1与种草面积x(m2)的函数关系式,y2与栽花面积x(m2)的函数关系式;
(2)设这块1000m2空地的绿化总费用为W(元),请利用W与种草面积x(m2)的函数关系式,求出绿化总费用W的最大值;
(3)若种草部分的面积不少于600m2,栽花部分的面积不少于200m2,请求出绿化总费用W的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为6,点E是正方形内部一点,连接BE,CE,且∠ABE=∠BCE,点P是边AB上一动点,连接PD,PE,则PD+PE的最小值为_____.
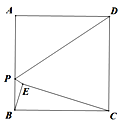
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 蜡烛在真空中燃烧是一个随机事件
B. 在射击比赛中,运动员射中靶心和没有射中靶心的可能性相同
C. 某抽奖游戏的中奖率为![]() ,说明只有抽奖100次,才能中奖1次
,说明只有抽奖100次,才能中奖1次
D. 天气预报明天降水概率为![]() ,表示明天下雨的可能性较大
,表示明天下雨的可能性较大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,半径BO与AC相交于点D,BO的延长线与⊙O交于点F,与过点C的切线NC交于点M,过点D作DE⊥BC,垂足为E,连接CF,已知MF=FC.
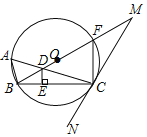
(1)求证:∠M=30°;
(2)①若![]() =
=![]() ,求
,求![]() 的值;
的值;
②当△DEC的面积是它最大值的![]() 时,求
时,求![]() 的值.
的值.
(3)若DE=![]() AB,试判断点D所在的位置.(请直接写出答案)
AB,试判断点D所在的位置.(请直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图(要求:以下操作均只使用无刻度的直尺)
(1)在直角坐标系中我们把横、纵坐标都为整数的点称为整点.如图1中点A(1,2)、B(3,4),在图1中第一象限内找出所有的整点P(图上标为P1、P2),使得点P横、纵坐标的平方和等于20.
(2)如图2,是大小相等的边长为1的正方形构成的网格,A、B、C、D均为格点.请在线段AD上找一点P,并连结BP使得直线BP将四边形ABCD的面积分为1:2两部分,在图中画出线段BP,并简要说明你的画图方法.
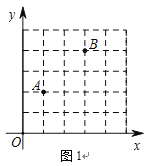
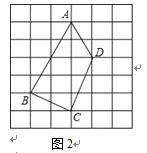
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx-3的图象与x轴交于点A(-1,0)和点B(3,0),顶点为D,点C是直线l:y=x+5与x轴的交点.
(1)求该二次函数的表达式;
(2)点E是直线l在第三象限上的点,连接EA、EB,当△ECA∽△BCE时,求E点的坐标;
(3)在(2)的条件下,连接AD、BD,在直线DE上是否存在点P,使得∠APD=∠ADB?若存在,求出点P的坐标;若不存在,请说明理由.
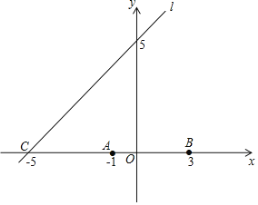
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系在代数和几何之间架起了一座桥梁,实现了几何方法与代数方法的结合,使数与形统一了起来,在平面直角坐标系中,已知点A(x1,y1)、B(x2,y2),则A、B两点之间的距离可以表示为AB=![]() ,例如A(2,1)、B(﹣1,2),则A、B两点之间的距离AB=
,例如A(2,1)、B(﹣1,2),则A、B两点之间的距离AB=![]() =
=![]() ;反之,代数式
;反之,代数式![]() 也可以看作平面直角坐标系中的点C(5,1)与点D(1,﹣2)之间的距离.
也可以看作平面直角坐标系中的点C(5,1)与点D(1,﹣2)之间的距离.
(1)已知点M(﹣7,6),N(1,0),则M、N两点间的距离为 ;
(2)求代数式![]() 的最小值;
的最小值;
(3)求代数式|![]() | 取最大值时,x的取值.
| 取最大值时,x的取值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com