
����Ŀ��ƽ��ֱ������ϵ�ڴ����ͼ���֮�������һ��������ʵ���˼��η�������������Ľ�ϣ�ʹ������ͳһ����������ƽ��ֱ������ϵ�У���֪��A��x1��y1����B��x2��y2������A��B����֮��ľ�����Ա�ʾΪAB��![]() ������A��2��1����B����1��2������A��B����֮��ľ���AB��
������A��2��1����B����1��2������A��B����֮��ľ���AB��![]() ��
��![]() ����֮������ʽ
����֮������ʽ![]() Ҳ���Կ���ƽ��ֱ������ϵ�еĵ�C��5��1�����D��1����2��֮��ľ��룮
Ҳ���Կ���ƽ��ֱ������ϵ�еĵ�C��5��1�����D��1����2��֮��ľ��룮
��1����֪��M����7��6����N��1��0������M��N�����ľ���Ϊ�� ����
��2�������ʽ![]() ����Сֵ��
����Сֵ��
��3�������ʽ|![]() | ȡ���ֵʱ��x��ȡֵ��
| ȡ���ֵʱ��x��ȡֵ��
���𰸡���1��10����2��13����3��![]()
��������
��1�����������ľ��빫ʽ���ɵõ����ۣ�
��2���ɣ�1����֪��![]() ��ʾx���ϵ�P��x��0�����E��-1��7���ľ���PE�͵�A��x��0�����F��4��5���ľ���PF֮�ͣ�����PE+PF����E����x��ԳƵ�
��ʾx���ϵ�P��x��0�����E��-1��7���ľ���PE�͵�A��x��0�����F��4��5���ľ���PF֮�ͣ�����PE+PF����E����x��ԳƵ�![]() ��-1��-7������Сֵ����
��-1��-7������Сֵ����![]() �����ɣ�1�����ɵõ����ۣ�
�����ɣ�1�����ɵõ����ۣ�
��3��������֪�����õ�![]() ���ɣ�1����֪��|
���ɣ�1����֪��|
��ʾ��A��x��0�����E��2��3���ľ���͵�A��x��0�����F��-![]() ��2���ľ���֮������ֵʱ����ֱ��EF��x��Ľ���ΪA��x��0�������ǵõ����ۣ�
��2���ľ���֮������ֵʱ����ֱ��EF��x��Ľ���ΪA��x��0�������ǵõ����ۣ�
�⣺��1���ߵ�M��-7��6����N��1��0����
��MN=![]() =10��
=10��
��M��N�����ľ�����10��
�ʴ�Ϊ��10��
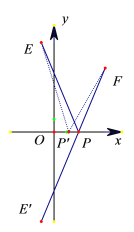
��2���ɣ�1����֪��![]() ��ʾ��P��x��0�����E��-1��7���ľ���͵�A��x��0�����F��4��5���ľ���֮�ͣ�
��ʾ��P��x��0�����E��-1��7���ľ���͵�A��x��0�����F��4��5���ľ���֮�ͣ�
����x���ҵ�һ�㵽EF�ĺ���С���ɽ�������ģ�Ϳ�֪���ԳƵ㣬��E����x��ԳƵ�![]() ��-1��-7��������
��-1��-7��������![]() ����AF+AE=
����AF+AE=![]() Ϊ��Сֵ��
Ϊ��Сֵ��
��![]() ��СֵΪ
��СֵΪ![]() �ij���
�ij���
��EF=![]() =13��
=13��
�����ʽ![]() ����Сֵ��13��
����Сֵ��13��
�ʴ�Ϊ13.
��3����![]() =
=![]() ��
��
���ɣ�1����֪��![]() ��ʾ��P��x��0�����E��2��3���ľ���PE�͵�P��x��0�����F��-
��ʾ��P��x��0�����E��2��3���ľ���PE�͵�P��x��0�����F��-![]() ��2���ľ���֮PF���|PE-PF|��P��E��F���㹲��ʱȡ���ֵʱ����ֱ��EF��x��Ľ���ΪA��x��0����
��2���ľ���֮PF���|PE-PF|��P��E��F���㹲��ʱȡ���ֵʱ����ֱ��EF��x��Ľ���ΪA��x��0����
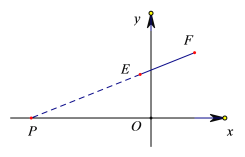
��ֱ��EF�Ľ���ʽΪy=kx+b��
��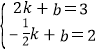 ��
��
��ã�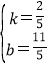 ��
��
��ֱ��EF�Ľ���ʽΪ![]()
��y=0ʱ��x=![]() ��
��
�����ʽ![]() ȡ���ֵʱ��x��ȡֵΪ
ȡ���ֵʱ��x��ȡֵΪ![]() ��
��


 ������ϵ�д�
������ϵ�д� �żӾ���ϵ�д�
�żӾ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��������������1�������n��������Щ�����ɫ�����������
��1���Ӵ����������һ����¼����ɫ��Ȼ��Żأ������ظ���ʵ�飬�������������Ƶ���ȶ���0.25����n��ֵ��
��2���ڣ�1���������£��Ӵ��������������������������ɫ��ͬ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
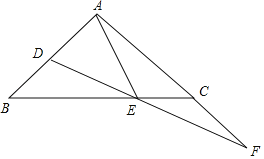
����Ŀ����ͼ����ABC�У�AB=AC����BAC=90�㣬��D��E�ֱ���AB��BC�ϣ���EAD=��EDA����FΪDE���ӳ�����AC���ӳ��ߵĽ��㣮
��1����֤��DE=EF��
��2���ж�BD��CF��������ϵ����˵�����ɣ�
��3����AB=3��AE=![]() ����BD�ij���
����BD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �У�
��![]() ����
����![]() �ڱ�
�ڱ�![]() �ϣ���
�ϣ���![]() ��
��![]() �˶����ٶ�Ϊ
�˶����ٶ�Ϊ![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() �룬��
�룬��![]() ����
����![]() ������
������![]() ����
����![]() ��Ӧ��Ϊ
��Ӧ��Ϊ![]() ��
��![]() ����ֱ�����
����ֱ�����![]() �����
�����![]() ��
��
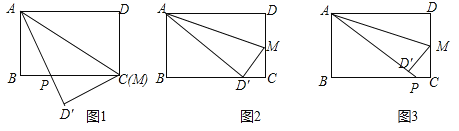
��1����ͼ![]() ����
����![]() ʱ����֤��
ʱ����֤��![]() ��
��
��2����ͼ![]() ����
����![]() Ϊ��ֵʱ����
Ϊ��ֵʱ����![]() ǡ�����ڱ�
ǡ�����ڱ�![]() �ϣ�
�ϣ�
��3����ͼ![]() ����
����![]() ʱ����
ʱ����![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC����E��F�ڱ�BC�ϣ�BE=CF����D��AF���ӳ����ϣ�AD=AC��
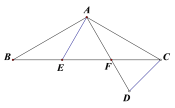
��1����֤����ABE����ACF��
��2������BAE=30�㣬���ADC= ��ֱ��д�𰸣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
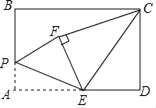
����Ŀ����ͼ������ABCD�У�AB��4��AD��6����EΪAD�е㣬��PΪ�߶�AB��һ�����㣬����EP������APE��PE�۵��õ���FPE������CE��CF������ECFΪֱ��������ʱ��AP�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=��x2+bx+c������A��B��C����֪A����1��0����C��0��3����
��1���������ߵĽ���ʽ��
��2����ͼ1��PΪ�߶�BC��һ�㣬����P��y��ƽ���ߣ����������ڵ�D������BDC��������ʱ�����P�����ꣻ
��3����ͼ2�������߶���ΪE��EF��x����F�㣬M��m��0����x����һ���㣬N���߶�EF��һ�㣬����MNC=90������ָ��ʵ��m�ı仯��Χ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ⷢ�֣�
��![]() ����ͼ�٣�
����ͼ�٣�![]() �У�
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��������һ�㣬��
��������һ�㣬��![]() ����СֵΪ__________��
����СֵΪ__________��
��![]() ����ͼ�ڣ�����
����ͼ�ڣ�����![]() �У�
��![]() ��
��![]() ����
����![]() ����
����![]() �ֱ���
�ֱ���![]() ��
��![]() �ϣ���
�ϣ���![]() ����Сֵ��
����Сֵ��
��![]() ����ͼ�ۣ�����
����ͼ�ۣ�����![]() �У�
��![]() ��
��![]() ����
����![]() ��
��![]() ����һ�㣬��
����һ�㣬��![]() ����
����![]() ��
��![]() ���ϵ�����һ�㣬��
���ϵ�����һ�㣬��![]() ��
��![]() ���ۣ���
���ۣ���![]() �Ķ�Ӧ��Ϊ��
�Ķ�Ӧ��Ϊ��![]() ������
������![]() ��
��![]() ���ı���
���ı���![]() ������Ƿ������Сֵ�������ڣ��������Сֵ����ʱ
������Ƿ������Сֵ�������ڣ��������Сֵ����ʱ![]() �ij��ȣ��������ڣ���˵�����ɣ�
�ij��ȣ��������ڣ���˵�����ɣ�



�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ѧϰ��ȫ�������ε��ж���������SSS����SAS����ASA��)�����Ǽ������������������������ߺ�����һ�ߵĶԽǶ�Ӧ����������ν����о�.
����˼�����������÷������Ա�ʾΪ������ABC����DEF�У�AC=DF��BC=EF����ABC=��DEF.Ȼ��ԡ�ABC���з��࣬�ɷ�Ϊ����ABC����ǡ�ֱ�ǡ��۽��������������̽����
��һ�����������ABC�����ʱ��AB=DE��һ��������
�ڶ������������ABC��ֱ��ʱ��������HL�����ɵ���ABC����DEF����AB=DE��
���������������ADC�Ƕ۽�ʱ����AB=DE.
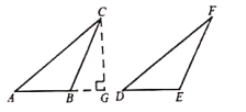
��ͼ������ABC����DEF�У�AC=DF��BC=EF����ABC=��DEF���ҡ�ABC�Ƕ۽ǣ���֤��AB=DE.
�������ɻ�����һ����Ч����ѧ˼ά��ʽ��һ���ǽ�δ���������ͨ������ת��Ϊ�ѽ��������.��Ⱥ���ֵ������������ת��Ϊ�ڶ����������ͼ������C��CG��AB��͢�����ڵ�G.
(1)����DEF���ó߹�����DE���ϵĸ�FH����д������������ͼ�ۼ���
(2)�������(1)����ͼ�Ļ����ϣ�����֤��AB=DE.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com