
����Ŀ���������ѧϰ��ȫ�������ε��ж���������SSS����SAS����ASA��)�����Ǽ������������������������ߺ�����һ�ߵĶԽǶ�Ӧ����������ν����о�.
����˼�����������÷������Ա�ʾΪ������ABC����DEF�У�AC=DF��BC=EF����ABC=��DEF.Ȼ��ԡ�ABC���з��࣬�ɷ�Ϊ����ABC����ǡ�ֱ�ǡ��۽��������������̽����
��һ�����������ABC�����ʱ��AB=DE��һ��������
�ڶ������������ABC��ֱ��ʱ��������HL�����ɵ���ABC����DEF����AB=DE��
���������������ADC�Ƕ۽�ʱ����AB=DE.
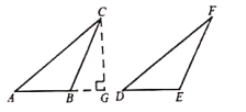
��ͼ������ABC����DEF�У�AC=DF��BC=EF����ABC=��DEF���ҡ�ABC�Ƕ۽ǣ���֤��AB=DE.
�������ɻ�����һ����Ч����ѧ˼ά��ʽ��һ���ǽ�δ���������ͨ������ת��Ϊ�ѽ��������.��Ⱥ���ֵ������������ת��Ϊ�ڶ����������ͼ������C��CG��AB��͢�����ڵ�G.
(1)����DEF���ó߹�����DE���ϵĸ�FH����д������������ͼ�ۼ���
(2)�������(1)����ͼ�Ļ����ϣ�����֤��AB=DE.
���𰸡���1������������2��������.
��������
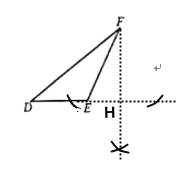
��1���߹���ͼ��FH��DE��DE�ӳ�����H���ɣ�
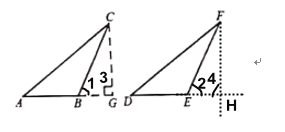
��2����֤����BCG����EFH,�õ�BG=EH����֤��Rt��ACG��Rt��DFH,�õ�AG=DH,Ȼ��ɵ�AB=DE.
�⣺(1)������FH����ͼ��ʾ��
��2��
��![]() ,
,
��![]() ,
,
�֡�CG��AG��FH��DH,
��![]() ,
,
�֡�BC=EF,
����BCG����EFH,
��BG=EH��CG=FH,
�֡�AC=DF,
��Rt��ACG��Rt��DFH,
��AG=DH,
�֡�BG=EH,
��AB=DE.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ�ڴ����ͼ���֮�������һ��������ʵ���˼��η�������������Ľ�ϣ�ʹ������ͳһ����������ƽ��ֱ������ϵ�У���֪��A��x1��y1����B��x2��y2������A��B����֮��ľ�����Ա�ʾΪAB��![]() ������A��2��1����B����1��2������A��B����֮��ľ���AB��
������A��2��1����B����1��2������A��B����֮��ľ���AB��![]() ��
��![]() ����֮������ʽ
����֮������ʽ![]() Ҳ���Կ���ƽ��ֱ������ϵ�еĵ�C��5��1�����D��1����2��֮��ľ��룮
Ҳ���Կ���ƽ��ֱ������ϵ�еĵ�C��5��1�����D��1����2��֮��ľ��룮
��1����֪��M����7��6����N��1��0������M��N�����ľ���Ϊ�� ����
��2�������ʽ![]() ����Сֵ��
����Сֵ��
��3�������ʽ|![]() | ȡ���ֵʱ��x��ȡֵ��
| ȡ���ֵʱ��x��ȡֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����һ��һ·�����ҳ��飬ij��·���˼�װ����������ʽ������2����������һ��ػ������ӹ̴���������2��8�������̹�˾�е����裬��֪2���̹�˾����������ɴ������Ҫ180��![]() ���̹�˾����ʩ�����
���̹�˾����ʩ�����![]() ���̹�˾��������������̹�˾�ֹ�ͬʩ��
���̹�˾��������������̹�˾�ֹ�ͬʩ��![]() �������˴����.
�������˴����.
��1����![]() ���̹�˾����������ɴ������Ҫ�����죿
���̹�˾����������ɴ������Ҫ�����죿
��2�������ܹ��̽��蹤�ڵ����ƣ���������ί�����������̻����������֣�Ҫ�������̹�˾ͬʱ������![]() ���̹�˾��������һ��������
���̹�˾��������һ��������![]() ����ɣ�
����ɣ�![]() ���̹�˾������һ��������
���̹�˾������һ��������![]() ����ɣ�����
����ɣ�����![]() ��
��![]() ������������
������������![]() ��
��![]() ����
����![]() ��
��![]() �������̹�˾��ʩ�������˶����죿
�������̹�˾��ʩ�������˶����죿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB��AC����BAC��45��������ABC�Ƶ�A��ʱ�뷽����ת����AEF�����У�E��F�ǵ�B��C��ת��Ķ�Ӧ�㣬BE��CF�ཻ�ڵ�D�����ı���ABDFΪ���Σ����CAE�Ĵ�С�ǣ�������
![]()
A. 45��B. 60��C. 75��D. 90��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ʵʩ��ҵ����ƶ������ƶ�����а���ɽ��ֲijƷ�����֣���֪�����ֵijɱ���Ϊ6Ԫ/ǧ�ˣ������ջ�Ͷ���г�����ʱ�������г�������ָ����ֲ����������ÿ���������y��ǧ�ˣ������۵���x��Ԫ��֮��ĺ�����ϵ��ͼ��ʾ��
��1����y��x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��
��2������Ʒ�����ֶ���Ϊ����ʱ��ÿ�����ۻ�õ����������������Ƕ��٣�
��3��ij��ũ�����깲��ժ����12000ǧ�ˣ�����Ʒ�����ֵı�����Ϊ50�죬���գ�2�������۷�ʽ���ܷ��ڱ�������ȫ���������������֣����ܣ���˵�����ɣ������ܣ�Ӧ�����ۼ�Ϊ����Ԫʱ���������������ܻ���������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x�ķ��̣�x��3����x��5��=m��m��0��������ʵ���������£�����������������ѡ����ȷ���ǣ�������
A. 3�������£�5 B. 3������5���� C. ����2���£�5 D. ����3���£�5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
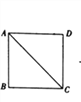
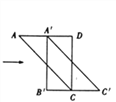
����Ŀ����ͼ�����߳�Ϊ12��������ABCD����Խ���AC�������ٰѡ�ABC����AD����ƽ�ƣ��õ���![]() ���������������ص������Ϊ32ʱ�������ƶ��ľ���
���������������ص������Ϊ32ʱ�������ƶ��ľ���![]() ����_____.
����_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90����AB=6��AD�ǡ�BAC��ƽ���ߣ�����A��D�����Բ��Բ��Oǡ������AB�ϣ���O�ֱ���AB��AC�ཻ�ڵ�E��F������O�İ뾶Ϊ2������Ӱ���ֵ������
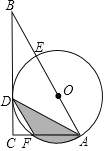
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com