
【题目】如图,△ABC内接于⊙O,半径BO与AC相交于点D,BO的延长线与⊙O交于点F,与过点C的切线NC交于点M,过点D作DE⊥BC,垂足为E,连接CF,已知MF=FC.
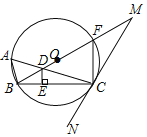
(1)求证:∠M=30°;
(2)①若![]() =
=![]() ,求
,求![]() 的值;
的值;
②当△DEC的面积是它最大值的![]() 时,求
时,求![]() 的值.
的值.
(3)若DE=![]() AB,试判断点D所在的位置.(请直接写出答案)
AB,试判断点D所在的位置.(请直接写出答案)
【答案】(1)证明见解析.(2)①![]() =
=![]() ,②
,②![]() =
=![]() .(3)点D与点O重合.
.(3)点D与点O重合.
【解析】
(1)连接OC,只要证明△FOC是等边三角形即可解决问题.
(2)①设OB=r,则DC=![]() OB=
OB=![]() r.作CH⊥BF于点H.想办法求出OD,OB即可解决问题.
r.作CH⊥BF于点H.想办法求出OD,OB即可解决问题.
②设⊙O的半径为r,DE=x,△DEC的面积为s.构建二次函数,利用二次函数的性质解决问题即可.
(3)连接OA.作OG⊥AB于G.由△GOB≌△EDC(AAS),推出OB=CD=OC,由∠BOC=∠OCM+∠M>90°,推出D,O,C三点无法构成等腰三角形,推出点D与点O重合.
解:(1)连接OC.
∵MN是切线,
∴∠MCO=90°,
∴∠MOC+∠M=90°=∠FCM+∠OCF,
∵MF=FC,
∴∠M=∠FCM,
∴∠MOC=∠OCF,
∴OF=CF=OC,
∴△FOC是等边三角形,
∴∠FOC=60°,
∴∠M=30°.
(2)①设OB=r,则DC=![]() OB=
OB=![]() r.
r.
作CH⊥BF于点H.
由(1)可知∠BFC=60°,FC=FO=OB=r,
∴∠FCH=30°,
在Rt△FCH中,FH=![]() FC=
FC=![]() ,CH=
,CH=![]() r,
r,
∴OH=![]() r,
r,
在Rt△CDH中,DH2+CH2=CD2,
∴DH2+(![]() r)2=(
r)2=(![]() r)2,
r)2,
∴DH=![]() r,
r,
∴OD=DH-OH=![]() r,∴
r,∴![]() =
=![]() .
.
②设⊙O的半径为r,DE=x,△DEC的面积为s.
由(1)可知∠B=![]() ∠FOC=30°,
∠FOC=30°,
∵DE⊥BC,
∴BE=![]() x,由垂径定理可得BC=
x,由垂径定理可得BC=![]() r,
r,
∴s=![]() x(
x(![]() r-
r-![]() x)=-
x)=-![]() x2+
x2+![]() rx.
rx.
∴当x=![]() r时,s有最大值,最大值=
r时,s有最大值,最大值=![]() r2,
r2,
当s=![]() ×
×![]() r2=
r2=![]() r2时,-
r2时,-![]() x2+
x2+![]() rx=
rx=![]() r2,
r2,
化简得到:9x2-9rx+2r2=0,
解得x=![]() r或
r或![]() r,
r,
∵x=DE=![]() BD≤
BD≤![]() r,
r,
∴r=![]() r,
r,
在Rt△DEC中,CD2=DE2+EC2=(![]() r)2+(
r)2+(![]() r-
r-![]() r)2=
r)2=![]() r2,
r2,
∴CD=![]() r,
r,
∴![]() =
=![]() .
.
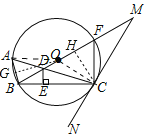
(3)连接OA.作OG⊥AB于G.
由垂径定理可知:GB=![]() AB,∠GOB=
AB,∠GOB=![]() ∠AOB,
∠AOB,
∵∠DCE=![]() ∠AOB,DE=
∠AOB,DE=![]() AB,
AB,
∴∠GOB=∠DCE,G=DE,
∵∠DGB=∠CED=90°
∴△GOB≌△EDC(AAS),
∴OB=CD=OC,
∵∠BOC=∠OCM+∠M>90°,
∴D,O,C三点无法构成等腰三角形,
∴点D与点O重合.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,![]() ,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
(1)求∠BAC的度数;
(2)当点D在AB上方,且CD⊥BP时,求证:PC=AC;
(3)在点P的运动过程中
①当点A在线段PB的中垂线上或点B在线段PA的中垂线上时,求出所有满足条件的∠ACD的度数;
②设⊙O的半径为6,点E到直线l的距离为3,连结BD,DE,直接写出△BDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,射线AP交⊙O于C点,∠PCO的平分线交⊙O于D点,过点D作![]() 交AP于E点.
交AP于E点.
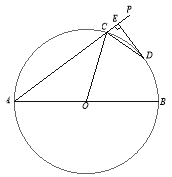
(1)求证:DE为⊙O的切线;
(2)若DE=3,AC=8,求直径AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有长为24m的篱笆,现一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为xm,面积为Sm2.
(1)求S与x的函数关系式及x值的取值范围;
(2)要围成面积为45m2的花圃,AB的长是多少米?
(3)当AB的长是多少米时,围成的花圃的面积最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明袋子中有1个红球和n个白球,这些球除颜色外无其他差别.
(1)从袋中随机摸出一个球,记录其颜色,然后放回.大量重复该实验,发现摸到红球的频率稳定于0.25,求n的值.
(2)在(1)的条件下,从袋中随机摸出两个球,求两个球颜色不同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.

(1)试说明DF是⊙O的切线;
(2)若AC=3AE,求tanC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线![]() 的一部分,如图
的一部分,如图
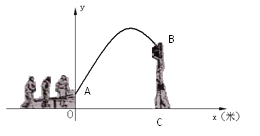
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
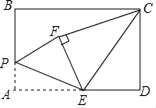
【题目】如图,矩形ABCD中,AB=4,AD=6,点E为AD中点,点P为线段AB上一个动点,连接EP,将△APE沿PE折叠得到△FPE,连接CE,CF,当△ECF为直角三角形时,AP的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com