Question

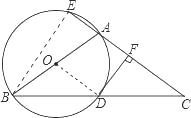
【题目】如图，△ABC中，AB=AC，以AB为直径的⊙O与BC相交于点D，与CA的延长线相交于点E，过点D作DF⊥AC于点F．

（1）试说明DF是⊙O的切线；

（2）若AC=3AE，求tanC．

Answer 1

【答案】（1）详见解析；（2）

【解析】试题分析：（1）连接OD，根据等边对等角得出∠B=∠ODB，∠B=∠C，得出∠ODB=∠C，证得OD∥AC，证得OD⊥DF，从而证得DF是⊙O的切线；

（2）连接BE，AB是直径，∠AEB=90°，根据勾股定理得出BE=2AE，CE=4AE，然后在RT△BEC中，即可求得tanC的值．

试题解析：（1）连接OD，

∵OB=OD，

∴∠B=∠ODB，

∵AB=AC，

∴∠B=∠C，

∴∠ODB=∠C，

∴OD∥AC，

∵DF⊥AC，

∴OD⊥DF，

∴DF是⊙O的切线；

（2）连接BE，

∵AB是直径，

∴∠AEB=90°，

∵AB=AC，AC=3AE，

∴AB=3AE，CE=4AE，

∴BE= ，

在RT△BEC中，tanC=．