
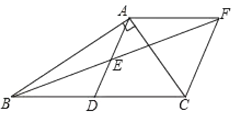
【题目】如图在![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() ;
;
(2)求证:四边形![]() 是菱形;
是菱形;
(3)若![]() ,求菱形
,求菱形![]() 的面积.
的面积.
科目:初中数学 来源: 题型:
【题目】随着绿城南宁近几年城市建设的快速发展,对花木的需求量逐年提高.某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润![]() 与投资量
与投资量![]() 成正比例关系,如图(1)所示;种植花卉的利润
成正比例关系,如图(1)所示;种植花卉的利润![]() 与投资量
与投资量![]() 成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)
成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)

(1)分别求出利润![]() 与
与![]() 关于投资量
关于投资量![]() 的函数关系式;
的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,他至少获得多少利润?他能获取的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点

(1)求证:△ABM≌△DCM
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD:AB= _时,四边形MENF是正方形(只写结论,不需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现:
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
(1)求证:△ACD≌△BCE;
(2)求证:CD∥BE.
拓展探究:
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,连接BE,求∠AEB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=3cm,BC=4cm. P、Q分别为AB、BC上的动点,点P从点A出发沿AB方向作匀速移动的同时,点Q从点B出发沿BC方向向点C作匀速移动,移动的速度均为1cm/s,设P、Q移动的时间为t(0<t≤4).
(1)当t为何值时,△BPQ与△ABC相似;
(2)当t为何值时,△BPQ是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.

(1)试说明DF是⊙O的切线;
(2)若AC=3AE,求tanC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光明中学准备购买一批笔袋奖励优秀同学.现文具店有A、B两种笔袋供选择,已知2个A笔袋和3个B笔袋的价格相同;而购买1个A笔袋和2个B笔袋共需35元.
(1)求A.B两种笔袋的单价;
(2)根据需要,学校共需购买40个笔袋,该文具店为了支持学校工作,给出了如下两种大幅优惠方案:方案一:A种笔袋六折、B种笔袋四折;方案二:A、B两种笔袋都五折.设购买A种笔袋个数为a(a≥0)个,购买这40个笔袋所需费用为w元.
①分别表示出两种优惠方案的情况下w与a之间的函数关系式;
②求出购买A种笔袋多少个时,两种方案所需费用一样多.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明星期天从家里出发骑车去舅舅家做客,当他骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,以下是他本次去舅舅家所用的时间与路程的关系式示意图,根据图中提供的信息回答下列问题:
(1)小明家到舅舅家的路程是______米,小明在商店停留了______分钟;
(2)在整个去舅舅家的途中哪个时间段小明骑车速度最快,最快的速度是多少米/
分?
(3)本次去舅舅家的行程中,小明一共行驶了多少米?一共用了多少分钟?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com