Question

【题目】如图，在△ABC中，∠C=90°，AC=3cm，BC=4cm. P、Q分别为AB、BC上的动点，点P从点A出发沿AB方向作匀速移动的同时，点Q从点B出发沿BC方向向点C作匀速移动，移动的速度均为1cm/s，设P、Q移动的时间为t（0＜t≤4）.

（1）当t为何值时，△BPQ与△ABC相似；

（2）当t为何值时，△BPQ是等腰三角形.

Answer 1

【答案】（1）t=或时，△BPQ与△ABC相似；（2）t=2.5或或.

【解析】试题分析：

（1）由已知条件易得AB=5，由于△BPQ和△ABC有公共角∠B，所以当或时，两三角形相似，由此可列出方程解得t的值；

（2）如图，由题意可知，需分三种情况讨论：①BP=BQ时，可直接列方程求得t的值；②BQ=PQ时，过点Q作QE⊥AB于点E，再证△BQE∽△BAC，从而可利用相似三角形的性质列比例式求出此时t的值；③PB=PQ时，过点P作PE⊥BC于点E，再证△PBE∽△ABC，从而可利用相似三角形的性质列比例式求出此时t的值.

试题解析：

（1）∵在△ABC中，∠C=90°，AC=3cm，BC=4cm.

∴AB=（cm）.

∵△BPQ和△ABC有公共角∠B，

∴①当时，△BPQ∽△BCA，由此可得： ，解得： ；

②当时，△BPQ∽△BAC，由此可得： ，解得： ；

∴当或时，△BPQ与△ABC相似；

（2）①如图1，当BP=BQ时，△BPQ是等腰三角形，由题意可得： ，解得： ；

②如图2，当BQ=PQ时，过点Q作QE⊥AB于点E，则BE=PE=BP=，∠BEQ=∠C=90°，

又∵∠B=∠B，

∴△BEQ∽△BCA，

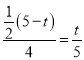∴，即 ，解得： ；

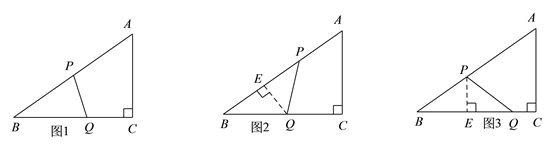
③如图3，当PB=PQ时，过点P作PE⊥BC于点E，则BE=EQ= ，∠BEP=∠C=90°，

又∵∠B=∠B，

∴△BEP∽△BCA，

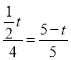∴，即，解得： ；

综上所述，当， ， 时，△BPQ是等腰三角形.