
����Ŀ���ڡ�ABC�У�DΪBC����һ�㣮
(1)��ͼ�٣���Rt��ABC�У���C��90�㣬����ABC����AD�۵�����C����AB���ϣ�����ֱ�ߺ�Բ��������D����д������������ͼ�ۼ�����
(2)��ͼ��������ABC���Ź���D��ֱ���۵�����C����AB���ϵ�E����
����DE��AB������ΪE������ֱ�ߺ�Բ��������D����д������������ͼ�ۼ�����
����AB��![]() ��BC��3����B��45�㣬��CD��ȡֵ��Χ��
��BC��3����B��45�㣬��CD��ȡֵ��Χ��

���𰸡���1�������������2�������������3��![]()
�������������������1������CAB�Ľ�ƽ�����ɣ�
��2��������C��CE��BC����BA���ӳ�����E������CEB�Ľ�ƽ�����ɣ�
������ͼ���У����CD����Сֵ������ͼ����E��A�غ�ʱ����AH��CB��H����CD=DE=x�����CD�ɵ�CD�����ֵ��
����������⣺��1����D��ͼ��ʾ��������CAB�Ľ�ƽ�����ɣ�
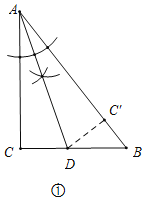
��2������D��ͼ��ʾ��������C��CE��BC����BA���ӳ�����E������CEB�Ľ�ƽ�����ɣ�
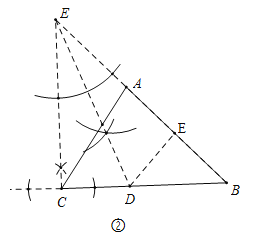
����ͼ���У���CD=DE=x����DE=EB=x����DEB=90����DB=![]() x����BC=3����x+
x����BC=3����x+![]() x=3����x=
x=3����x=![]() ����ͼ���У���E��A�غ�ʱ����AH��CB��H����CD=DE=x��
����ͼ���У���E��A�غ�ʱ����AH��CB��H����CD=DE=x��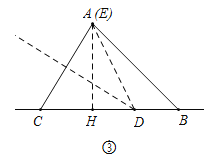
��Rt��AHB�У���֪AH=HB=2����AHB=90����HD=x��1��DE=x����x2=22+��x��1��2����x=![]() ��
��
���Ͽ�֪��CD�����ֵΪ![]() ����СֵΪ
����СֵΪ![]() ����
����![]() ��CD��
��CD��![]() ���ʴ�Ϊ��
���ʴ�Ϊ�� ![]() ��CD��
��CD��![]() ��
��


 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=kx+b������A��5��0����B��1��4����

��1����ֱ��AB�Ľ���ʽ��
��2����ֱ��y=2x��4��ֱ��AB�ཻ�ڵ�C�����C�����ꣻ
��3������ͼ��д������x�IJ���ʽ2x��4��kx+b�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ӵ���һ��ѡ��һ����Ա.�������������������ͬѧ����5��3����Ͷ������,ÿ��ÿ��Ͷ10����,ͼ��¼����������ͬѧ5��Ͷ����Ͷ�еĸ���.

(1)�������ͼ�е�����,��д�±�;
���� | ƽ���� | ���� | ���� |
���� | 7 | ||
��� | 7 | 2.8 |
(2)����Ϊ˭�ijɼ��Ƚ��ȶ�,Ϊʲô?
(3)�����ǽ���,�����ѡ˭?��Ҫ˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C=90����AC=3cm��BC=4cm. P��Q�ֱ�ΪAB��BC�ϵĶ��㣬��P�ӵ�A������AB�����������ƶ���ͬʱ����Q�ӵ�B������BC�������C�������ƶ����ƶ����ٶȾ�Ϊ1cm/s����P��Q�ƶ���ʱ��Ϊt��0��t��4��.
��1����tΪ��ֵʱ����BPQ���ABC������
��2����tΪ��ֵʱ����BPQ�ǵ���������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ�е�С�����DZ߳�Ϊ1�������Σ���ABC�Ķ����O�㶼�������εĶ����ϣ�
��1���Ե�OΪλ�����ģ��ڷ���ͼ�н���ABC�Ŵ�Ϊԭ����2�����õ���A��B��C����
��2����A��B��C���Ƶ�B��˳ʱ����ת90����������ת��õ�����A��B��C���������A��B������ת������ɨ����ͼ�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧ������һ���ʴ���������ͬѧ�����ľߵ���A��B���ֱʴ���ѡ����֪2��A�ʴ���3��B�ʴ��ļ۸���ͬ��������1��A�ʴ���2��B�ʴ�����35Ԫ��
��1����A��B���ֱʴ��ĵ��ۣ�
��2��������Ҫ��ѧУ���蹺��40���ʴ������ľߵ�Ϊ��֧��ѧУ�������������������ִ���Żݷ���������һ��A�ֱʴ����ۡ�B�ֱʴ����ۣ���������A��B���ֱʴ������ۣ��蹺��A�ֱʴ�����Ϊa��a��0������������40���ʴ��������ΪwԪ��
�ٷֱ��ʾ�������Żݷ����������w��a֮��ĺ�����ϵʽ��
���������A�ֱʴ����ٸ�ʱ�����ַ����������һ���࣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
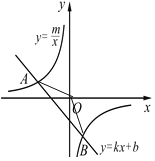
����Ŀ����ͼ����֪A(-4��2)��B(n��-4)��һ�κ���![]() ��ͼ���뷴��������
��ͼ���뷴��������![]() ��ͼ�����������.
��ͼ�����������.
��1����˷�����������һ�κ����Ľ���ʽ��
��2�����AOB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��
��![]() �ύ��A��B���㣬��
�ύ��A��B���㣬��![]() �ύ�ڵ�C�������ߵĶԳ��ύ
�ύ�ڵ�C�������ߵĶԳ��ύ![]() ���ڵ�D����֪A(-1��0)��C(0��2) .
���ڵ�D����֪A(-1��0)��C(0��2) .
��1���������ߵĽ���ʽ��
��2����E���߶�BC�ϵ�һ�����㣨����B��C�غϣ�������E��![]() ��Ĵ������������ཻ�ڵ�F������E�˶���ʲôλ��ʱ���ı���CDBF������������ı���CDBF������������ʱ��E������.
��Ĵ������������ཻ�ڵ�F������E�˶���ʲôλ��ʱ���ı���CDBF������������ı���CDBF������������ʱ��E������.
��3���������ߵĶԳ������Ƿ���ڵ�P��ʹ��PCD����CDΪ���ĵ��������Σ�������ڣ�ֱ��д��P������ꣻ��������ڣ���˵������.
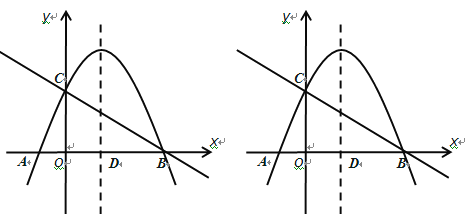
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ڡ�ABC�У�AB��AC��BC��12���ף���DΪAB��һ����BD��8���ף���P���߶�BC����2����/����ٶ���B����C���˶������˶�ʱ��Ϊt��ͬʱ����Q���߶�CA����C����A���˶�.

��1���ú�t��ʽ�ӱ�ʾPC�ij�Ϊ_______________;
��2������Q���˶��ٶ����p���˶��ٶ���ȣ���t��2ʱ��������BPD��������CQP�Ƿ�ȫ�ȣ���˵�����ɣ�
��3������Q���˶��ٶ����P���˶��ٶȲ���ȣ��������Q���˶��ٶ��Ƕ���ʱ���ܹ�ʹ������BPD��������CQPȫ��?
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com