
【题目】有长为24m的篱笆,现一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为xm,面积为Sm2.
(1)求S与x的函数关系式及x值的取值范围;
(2)要围成面积为45m2的花圃,AB的长是多少米?
(3)当AB的长是多少米时,围成的花圃的面积最大?
【答案】(1)S=﹣3x2+24x(![]() );(2)AB长为5m;(3)当AB=
);(2)AB长为5m;(3)当AB=![]() m时,围成的花圃的面积最大.
m时,围成的花圃的面积最大.
【解析】
(1)设花圃宽AB为xm,则长为(24-3x),利用长方形的面积公式,可求出S与x关系式,根据墙的最大长度求出x的取值范围;
(2)根据(1)所求的关系式把S=45代入即可求出x,即AB;
(3)根据二次函数的性质及x的取值范围求出即可.
解:(1)根据题意,得S=x(24﹣3x),
即所求的函数解析式为:S=﹣3x2+24x,
又∵0<24﹣3x≤10,
∴![]() ;
;
(2)根据题意,设花圃宽AB为xm,则长为(24-3x),
∴﹣3x2+24x=45.
整理,得x2﹣8x+15=0,
解得x=3或5,
当x=3时,长=24﹣9=15>10不成立,
当x=5时,长=24﹣15=9<10成立,
∴AB长为5m;
(3)S=24x﹣3x2=﹣3(x﹣4)2+48
∵墙的最大可用长度为10m,0≤24﹣3x≤10,
∴![]() ,
,
∵对称轴x=4,开口向下,
∴当x=![]() m,有最大面积的花圃.
m,有最大面积的花圃.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
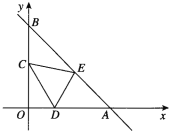
【题目】已知:如图,直线y=-x+12分别交x轴、y轴于A、B点,将△AOB折叠,使A点恰好落在OB的中点C处,折痕为DE.
(1)求AE的长及sin∠BEC的值;
(2)求△CDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
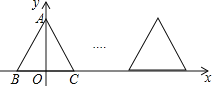
【题目】已知等边三角形ABC在平面直角坐标系中的位置如图所示,C(1,0),点A在y轴的正半轴上,把等边三角形ABC沿x轴正半轴作无滑动的连续翻转,每次翻转120°,经过2018次翻转之后,点C的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知方程![]() ,
,
(1)求证:方程一定有两个不相等的实数根;
(2)![]() 取何值时,方程二根中一个比3大,一个比3小。(可用数形结合来解)
取何值时,方程二根中一个比3大,一个比3小。(可用数形结合来解)
(3)![]() 取何值时方程的两个根异号且负的实数根的绝对值大.
取何值时方程的两个根异号且负的实数根的绝对值大.
查看答案和解析>>
科目:初中数学 来源: 题型:
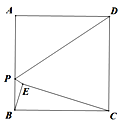
【题目】如图,正方形ABCD的边长为6,点E是正方形内部一点,连接BE,CE,且∠ABE=∠BCE,点P是边AB上一动点,连接PD,PE,则PD+PE的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
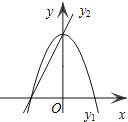
【题目】如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1,y2.若y1≠y2,取y1,y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.那么使得M=1的x值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,半径BO与AC相交于点D,BO的延长线与⊙O交于点F,与过点C的切线NC交于点M,过点D作DE⊥BC,垂足为E,连接CF,已知MF=FC.
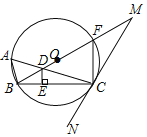
(1)求证:∠M=30°;
(2)①若![]() =
=![]() ,求
,求![]() 的值;
的值;
②当△DEC的面积是它最大值的![]() 时,求
时,求![]() 的值.
的值.
(3)若DE=![]() AB,试判断点D所在的位置.(请直接写出答案)
AB,试判断点D所在的位置.(请直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b的图象与反比例函数y2=![]() 的图象交于A(m,3),B(-3,n)两点.
的图象交于A(m,3),B(-3,n)两点.
(1)求一次函数的解析式;
(2)观察函数图象,直接写出关于x的不等式![]() >kx+b的解集.
>kx+b的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
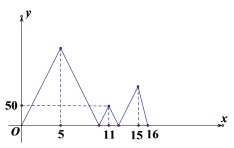
【题目】小亮和小花约定周六早晨在一直线公路AB上进行(A→B→A)往返跑训练,两人同时从A点出发,小亮以较快的速度匀速跑到点B休息1分钟后立即原速跑回A点,小花先匀速慢跑了5分钟后,把速度提高到原来的![]() 倍,又经过6分钟后超越了小亮一段距离,小花又将速度降低到出发时的速度,并以这一速度匀速跑到B点看到休息的小亮,然后立即以出发时的速度跑回A点.若两人之间的距离记为y(米),小花的跑步时间记为x(分),y和x的部分函数关系如图所示,则当小亮回到A点时小花距A点________米.
倍,又经过6分钟后超越了小亮一段距离,小花又将速度降低到出发时的速度,并以这一速度匀速跑到B点看到休息的小亮,然后立即以出发时的速度跑回A点.若两人之间的距离记为y(米),小花的跑步时间记为x(分),y和x的部分函数关系如图所示,则当小亮回到A点时小花距A点________米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com