已知正比例函数y1=2x和一次函数y2=-x+b,一次函数的图象与x轴、y轴分别交于点A、点B,正比例函数的图象与一次函数的图象相交于点P.
(1)若P点坐标为(3,n),试求一次函数的表达式,并用图象法求y1≥y2的解;
(2)若S△AOP=3,试求这个一次函数的表达式;
(3)x轴上有一定点E(2,0),若△POB≌△EPA,求这个一次函数的表达式.
解:(1)∵正比例函数y
1=2x和一次函数y
2=-x+b的图象相交于点P,P点坐标为(3,n),
∴代入正比例函数求得n=6,
∴点P的坐标为(3,6),
∴代入y
2=-x+b得b=9,
所以一次函数的表达式为y
2=-x+9;
图象为:

∴y
1≥y
2的解为:x≤3;
(2)∵一次函数y
2=-x+b的图象与x轴、y轴分别交于点A(b,0)、点B(0,b),两函数的图象交与点(

,
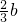
),
∴S
△AOP=

×b×
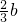
=3,
解得:b=±3,
所以一次函数的表达式为:y
2=-x±3;
(3)当b>0时,如图:
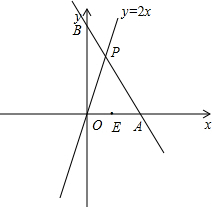
∵△POB≌△EPA,
∴PO=PE,
∵E(2,0),
∴点P的横坐标为1,
∵点P在y=2x上,
∴点P的纵坐标为2,
∴点P的坐标为(1,2),
∴代入y
2=-x+b得:y
2=-x+3;
当b<0时,如图:

∵△POB≌△EPA,
∴PO=PE,
∵点P在第三象限,
∴不成立;
综上所叙:若△POB≌△EPA时,一次函数的表达式为y=-x+3.
分析:(1)将点P的坐标代入到正比例函数中求得n值,然后代入到一次函数中即可确定其表达式,然后根据其图象的位置和交点坐标确定不等式的解集;
(2)用b表示出点A和点P的坐标,根据S
△AOP=3求得点P的坐标即可求得一次函数的表达式;
(3)分一次函数经过一、二、四象限和经过二、三、四象限两种情况并利用全等三角形的性质求得一次函数的表达式即可.
点评:本题考查了一次函数的综合知识,特别是本题中与三角形的面积的知识相结合使得问题变难,此类题目往往是中考的压轴题,应该重点掌握.


 ,
,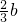 ),
), ×b×
×b×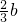 =3,
=3,



 名校课堂系列答案
名校课堂系列答案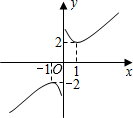 象似双钩,我们称之为“双钩函数”).给出下列几个命题:
象似双钩,我们称之为“双钩函数”).给出下列几个命题: 已知正比例函数y1=x,反比例函数y2=
已知正比例函数y1=x,反比例函数y2=