
【题目】如图,把一个转盘分成六等份,依次标上数字1、2、3、4、5、6,小明和小芳分别只转动一次转盘.小明同学先转动转盘,结果指针指向2,接下来小芳转动转盘,若把小明和小芳转动转盘指针指向的数字分别记作![]() 、
、![]() ,把
,把![]() 、
、![]() 作为点
作为点![]() 的横、纵坐标.
的横、纵坐标.

(1)写出点![]() 所有可能的坐标;
所有可能的坐标;
(2)求点![]() 在直线
在直线![]() 上的概率.
上的概率.
科目:初中数学 来源: 题型:
【题目】小王家新买的一套住房的建筑平面图如图所示(单位:米).
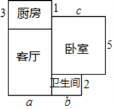
(1)这套住房的建筑总面积是多少平方米?(用含a,b,c的式子表示)
(2)若a=7.5,b=5,c=6,试求出小王家这套住房的具体面积.
(3)地面装修要铺设瓷砖,公司报价是:客厅地面每平方米180元,卧室地面每平方米150元,厨房地面每平方米120元,卫生间地面每平方米85元.在(2)的条件下,小王一共要花多少钱?
(4)这套住房的售价为每平方米4500元,购房时首付款为房价的40%,余款向银行申请贷款,在(2)的条件下,小王家购买这套住房时向银行申请贷款的金额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解决“经过平面上的100个点中的任意两点最多能画出多少条直线”这个问题,数学课外兴趣小组的同学们讨论得出如下方法:当![]() 时,画出最多直线的条数分别是:
时,画出最多直线的条数分别是:
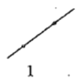
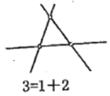
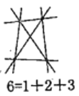
过两点画一条直线,三点在原来的基础上增加一个点,它与原来两点分别画一条直线,即增加两条直线,以此类推,平面上的10个点最多能画出![]() 条直线.
条直线.
请你比照上述方法,解决下列问题:(要求作图分析)
(1)平面上的20条直线最多有多少个交点?
(2)平面上的100条直线最多可以把平面分成多少个部分?平面上![]() 条直线最多可以把平面分成多少个部分?
条直线最多可以把平面分成多少个部分?
查看答案和解析>>
科目:初中数学 来源: 题型:
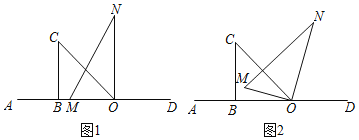
【题目】将一副直角三角板按如图1摆放在直线AD上![]() 直角三角板OBC和直角三角板MON,
直角三角板OBC和直角三角板MON,![]() ,
,![]() ,
,![]() ,
,![]() ,保持三角板OBC不动,将三角板MON绕点O以每秒
,保持三角板OBC不动,将三角板MON绕点O以每秒![]() 的速度顺时针方向旋转t秒
的速度顺时针方向旋转t秒![]()
![]() 如图2,
如图2,![]() ______度
______度![]() 用含t的式子表示
用含t的式子表示![]() ;
;
![]() 在旋转的过程中,是否存在t的值,使
在旋转的过程中,是否存在t的值,使![]() ?若存在,请求出t的值;若不存在,请说明理由.
?若存在,请求出t的值;若不存在,请说明理由.
![]() 直线AD的位置不变,若在三角板MON开始顺时针旋转的同时,另一个三角板OBC也绕点O以每秒
直线AD的位置不变,若在三角板MON开始顺时针旋转的同时,另一个三角板OBC也绕点O以每秒![]() 的速度顺时针旋转.
的速度顺时针旋转.
![]() 当
当![]() ______秒时,
______秒时,![]() ;
;
![]() 请直接写出在旋转过程中,
请直接写出在旋转过程中,![]() 与
与![]() 的数量关系
的数量关系![]() 关系式中不能含
关系式中不能含![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成一项工作,如果安排两个人合做,要![]() 天才能完成.开始先安排一些人做
天才能完成.开始先安排一些人做![]() 天后,又增加
天后,又增加![]() 人和他们一起做
人和他们一起做![]() 天,结果完成了这项工作的一半,假设这些人的工作效率相同.
天,结果完成了这项工作的一半,假设这些人的工作效率相同.
(1)开始安排了多少名工人?
(2)如果要求再用![]() 天做完剩余的全部工作,还需要再增加几人一起做?
天做完剩余的全部工作,还需要再增加几人一起做?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张直角三角形纸片![]() 沿斜边
沿斜边![]() 上的中线
上的中线![]() 剪开,得到
剪开,得到![]() ,再将
,再将![]() 沿
沿![]() 方向平移到
方向平移到![]() 的位置,若从平移开始到点
的位置,若从平移开始到点![]() 未到达点
未到达点![]() 时,
时,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() .
.
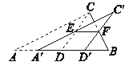
(1)试探究![]() 的形状,请说明理由;
的形状,请说明理由;
(2)当四边形![]() 为菱形时,判断
为菱形时,判断![]() 与
与![]() 是否全等,请说明理由.
是否全等,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学问题:用边长相等的正三角形、正方形和正六边形能否进行平面图形的镶嵌?
问题探究:为了解决上述数学问题,我们采用分类讨论的思想方法去进行探究.
探究一:从正三角形、正方形和正六边形中任选一种图形,能否进行平面图形的镶嵌?
第一类:选正三角形.因为正三角形的每一个内角是60°,所以在镶嵌平面时,围绕某一点有6个正三角形的内角可以拼成一个周角,所以用正三角形可以进行平面图形的镶嵌.
第二类:选正方形.因为正方形的每一个内角是90°,所以在镶嵌平面时,围绕某一点有4个正方形的内角可以拼成一个周角,所以用正方形也可以进行平面图形的镶嵌.
第三类:选正六边形.(仿照上述方法,写出探究过程及结论)
探究二:从正三角形、正方形和正六边形中任选两种图形,能否进行平面图形的镶嵌?
第四类:选正三角形和正方形
在镶嵌平面时,设围绕某一点有x个正三角形和y个正方形的内角可以拼成个周角.根据题意,可得方程
60x+90y=360
整理,得2x+3y=12.
我们可以找到唯一组适合方程的正整数解为![]() .
.
镶嵌平面时,在一个顶点周围围绕着3个正三角形和2个正方形的内角可以拼成一个周角,所以用正三角形和正方形可以进行平面镶嵌
第五类:选正三角形和正六边形.(仿照上述方法,写出探究过程及结论)
第六类:选正方形和正六边形,(不写探究过程,只写出结论)
探究三:用正三角形、正方形和正六边形三种图形是否可以镶嵌平面?
第七类:选正三角形、正方形和正六边形三种图形.(不写探究过程,只写结论),
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com