
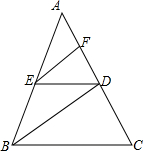
 如图,BD是∠ABC的平分线,ED∥BC,∠FED=∠BDE,
如图,BD是∠ABC的平分线,ED∥BC,∠FED=∠BDE,分析 先利用角平分线定义得到∠ABD=∠CBD,再根据平行线的性质由ED∥BC得∠EDB=∠CBD,则∠ABD=∠EDB,接着由∠FED=∠BDE可判断EF∥BD,则利用平行线的性质得∠EDB=∠DEF,∠ABD=∠AEF,所以∠AEF=∠DEF,从而得到结论.
解答 证明:∵BD是∠ABC的平分线,
∴∠ABD=∠CBD,
∵ED∥BC,
∴∠EDB=∠CBD,
∴∠ABD=∠EDB,
∵∠FED=∠BDE,
∴EF∥BD,
∴∠EDB=∠DEF,∠ABD=∠AEF,
∴∠AEF=∠DEF,
∴EF是∠AED的平分线.
点评 本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:初中数学 来源: 题型:解答题
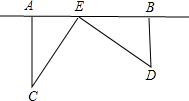 为了丰富少年儿童的业余生活,某社区要在如图中的AB所在的直线上建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B.已知AB=2.5km,CA=1.5km,DB=1.0km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?
为了丰富少年儿童的业余生活,某社区要在如图中的AB所在的直线上建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B.已知AB=2.5km,CA=1.5km,DB=1.0km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
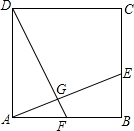 如图,已知点E、F分别为正方形ABCD的边BC、AB上的点,且AF=BE,AE与DF交于点G,试猜想AE与DF之间的大小关系和位置关系,并证明你的猜想.
如图,已知点E、F分别为正方形ABCD的边BC、AB上的点,且AF=BE,AE与DF交于点G,试猜想AE与DF之间的大小关系和位置关系,并证明你的猜想.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com