
【题目】如图,在平面直角坐标系中,点C(0,4),射线CE∥x轴,直线y=﹣ ![]() x+b交线段OC于点B,交x轴于点A,D是射线CE上一点.若存在点D,使得△ABD恰为等腰直角三角形,则b的值为 .
x+b交线段OC于点B,交x轴于点A,D是射线CE上一点.若存在点D,使得△ABD恰为等腰直角三角形,则b的值为 . 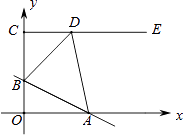
【答案】![]() 或
或 ![]() 或2
或2
【解析】解:①当∠ABD=90°时,如图1,则∠DBC+∠ABO=90°, 
∴∠DBC=∠BAO,
由直线y=﹣ ![]() x+b交线段OC于点B,交x轴于点A可知OB=b,OA=2b,
x+b交线段OC于点B,交x轴于点A可知OB=b,OA=2b,
∵点C(0,4),
∴OC=4,
∴BC=4﹣b,
在△DBC和△BAO中,
∴△DBC≌△BAO(AAS),
∴BC=OA,
即4﹣b=2b,
∴b= ![]() ;
;
②当∠ADB=90°时,如图2,
作AF⊥CE于F,
同理证得△BDC≌△DAF,
∴CD=AF=4,BC=DF,
∵OB=b,OA=2b,
∴BC=DF=2b﹣4,
∵BC=4﹣b,
∴2b﹣4=4﹣b,
∴b= ![]() ;
;
③当∠DAB=90°时,如图3,
作DF⊥OA于F,
同理证得△AOB≌△DFA,
∴OA=DF,
∴2b=4,
∴b=2;
综上,b的值为 ![]() 或
或 ![]() 或2.
或2.
所以答案是 ![]() 或
或 ![]() 或2.
或2.
【考点精析】根据题目的已知条件,利用等腰直角三角形的相关知识可以得到问题的答案,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k+1)x+4(k﹣![]() )=0.
)=0.
(1)判断这个一元二次方程的根的情况;
(2)若等腰三角形的一边长为3,另两条边的长恰好是这个方程的两个根,求这个等腰三角形的周长及面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程![]() ﹣1的步骤如下:
﹣1的步骤如下:
(解析)第一步:![]() ﹣1(分数的基本性质)
﹣1(分数的基本性质)
第二步:2x﹣1=3(2x+8)﹣3……(①)
第三步:2x﹣1=6x+24﹣3……(②)
第四步:2x﹣6x=24﹣3+1……(③)
第五步:﹣4x=22(④)
第六步:x=﹣![]() ……(⑤)
……(⑤)
以上解方程第二步到第六步的计算依据有:①去括号法则.②等式性质一.③等式性质二.④合并同类项法则.请选择排序完全正确的一个选项( )
A. ②①③④② B. ②①③④③ C. ③①②④③ D. ③①④②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A( ![]() ,0),B(3
,0),B(3 ![]() ,2),C(0,2).动点D以每秒1个单位的速度从点O出发沿OC向终点C运动,同时动点E以每秒2个单位的速度从点A出发沿AB向终点B运动.过点E作EF⊥AB,交BC于点F,连接DA、DF.设运动时间为t秒.
,2),C(0,2).动点D以每秒1个单位的速度从点O出发沿OC向终点C运动,同时动点E以每秒2个单位的速度从点A出发沿AB向终点B运动.过点E作EF⊥AB,交BC于点F,连接DA、DF.设运动时间为t秒.
(1)求∠ABC的度数;
(2)当t为何值时,AB∥DF;
(3)设四边形AEFD的面积为S.①求S关于t的函数关系式;
②若一抛物线y=﹣x2+mx经过动点E,当S<2 ![]() 时,求m的取值范围(写出答案即可).
时,求m的取值范围(写出答案即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为坐标原点,点A、B、C的坐标分别为A( ![]() ,0)、B(3
,0)、B(3 ![]() ,0)、C(0,5),点D在第一象限内,且∠ADB=60°,则线段CD的长的最小值是( )
,0)、C(0,5),点D在第一象限内,且∠ADB=60°,则线段CD的长的最小值是( )
A.2 ![]() ﹣2
﹣2
B.2 ![]()
C.2 ![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为24厘米.甲、乙两动点同时从顶点A出发,甲以2厘米/秒的速度沿正方形的边按顺时针方向移动,乙以4厘米/秒的速度沿正方形的边按逆时针方向移动,每次相遇后甲乙的速度均增加1厘米/秒且都改变原方向移动,则第四次相遇时甲与最近顶点的距离是______厘米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有两根直杆隔河相对,杆CD高30m,杆AB高20m,两杆相距50m.现两杆上各有一只鱼鹰,它们同时看到两杆之间的河面上E处浮起一条小鱼,于是以同样的速度同时飞下来夺鱼,结果两只鱼鹰同时到达,叼住小鱼.问两杆底部距鱼的距离各是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】细心观察下图,认真分析各式,然后解答问题.
(![]() )2+1=2,S1=
)2+1=2,S1=![]() ;
;
(![]() )2+1=3,S2=
)2+1=3,S2=![]() ;
;
(![]() )2+1=4,S3=
)2+1=4,S3=![]() .
.
(1)请用含n(n是正整数)的等式表示上述式子的变化规律;
(2)推算出OA10的长;
(3)求出S12+S22+S32+…+S102的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(4,0),B(0,4 ![]() ),把一个直角三角尺DEF放在△OAB内,使其斜边FD在线段AB上,三角尺可沿着线段AB上下滑动.其中∠EFD=30°,ED=2,点G为边FD的中点.
),把一个直角三角尺DEF放在△OAB内,使其斜边FD在线段AB上,三角尺可沿着线段AB上下滑动.其中∠EFD=30°,ED=2,点G为边FD的中点.
(1)求直线AB的解析式;
(2)如图1,当点D与点A重合时,求经过点G的反比例函数y= ![]() (k≠0)的解析式;
(k≠0)的解析式;
(3)在三角尺滑动的过程中,经过点G的反比例函数的图象能否同时经过点F?如果能,求出此时反比例函数的解析式;如果不能,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com