
【题目】如图1,已知A(0,a),B(b,0),且a、b满足a2﹣4a+20=8b﹣b2 . 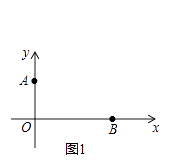
(1)求A、B两点的坐标;
(2)如图2,连接AB,若D(0,﹣6),DE⊥AB于点E,B、C关于y轴对称,M是线段DE上的一点,且DM=AB,连接AM,试判断线段AC与AM之间的位置和数量关系,并证明你的结论; 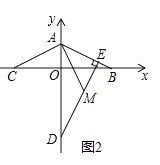
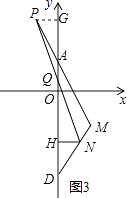
(3)如图3,在(2)的条件下,若N是线段DM上的一个动点,P是MA延长线上的一点,且DN=AP,连接PN交y轴于点Q,过点N作NH⊥y轴于点H,当N点在线段DM上运动时,△MQH的面积是否为定值?若是,请求出这个值;若不是,请说明理由. 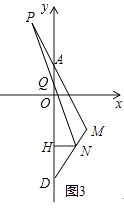
【答案】
(1)解:∵a2﹣4a+20=8b﹣b2,
∴(a﹣2)2+(b﹣4)2=0,
∴a=2,b=4,
∴A(0,2),B(4,0)
(2)解:∵AD=OA+OD=8,BC=2OB=8,
∴AD=BC,
在△CAB与△AMD中,  ,
,
∴△CAB≌△AMD,
∴AC=AM,∠ACO=∠MAD,
∵∠ACO+∠CAO=90°,
∴∠MAD+∠CAO=∠MAC=90°,
∴AC=AM,AC⊥AM
(3)解:过P作PG⊥y轴于G,
在△PAG与△HND中, 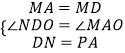 ,
,
∴△PAG≌△HND,
∴PG=HN,AG=HD,
∴AD=GH=8,
在△PQG与△NHQ中, 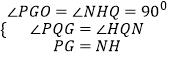 ,
,
∴△PQG≌△NHQ,
∴QG=QH= ![]() GH=4,
GH=4,
∴S△MQH= ![]() ×4×2=4.
×4×2=4.
【解析】(1)由a2﹣4a+20=8b﹣b2 , 得到(a﹣2)2+(b﹣4)2=0,求得a=2,b=4,于是得到结论;(2)由已知条件得到AD=BC,推出△CAB≌△AMD,根据全等三角形的性质得到AC=AM,∠ACO=∠MAD,由于∠ACO+∠CAO=90°,得到∠MAD+∠CAO=∠MAC=90°即可得到结论;(3)过P作PG⊥y轴于G,证得△PAG≌△HND,根据全等三角形的性质得到PG=HN,AG=HD,证得△PQG≌△NHQ,得到QG=QH= ![]() GH=4即可得到结论.
GH=4即可得到结论.


科目:初中数学 来源: 题型:
【题目】阅读下列文字:
我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如由图1可以得到(a+2b)(a+b)=a2+3ab+2b2 .
请解答下列问题: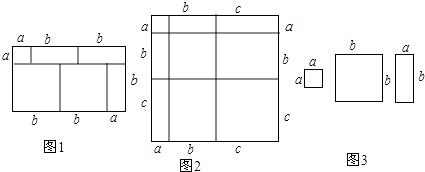
(1)写出图2中所表示的数学等式;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=12,ab+bc+ac=42,求a2+b2+c2的值;
(3)图3中给出了若干个边长为a和边长为b的小正方形纸片及若干个边长分别为a、b的长方形纸片,请利用所给的纸片拼出一个几何图形,使得用两种不同的方法计算它的面积时,能够得到数学公式:2a2+7ab+3b2=(a+3b)(2a+b).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.两个位似图形对应点连线有可能无交点
B.两个位似图形对应点连线交点个数为1或2
C.两个位似图形对应点连线只有一个交点
D.两个位似图形对应点连线交点个数不少于4个
查看答案和解析>>
科目:初中数学 来源: 题型:
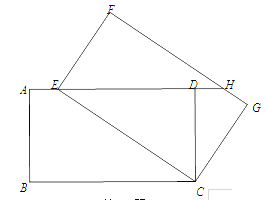
【题目】如图,将矩形ABCD绕点C旋转得到矩形FECG,点E在AD上,延长ED交FG于点H.
(1)求证:△EDC≌△HFE;
(2)连接BE、CH.
①四边形BEHC是怎样的特殊四边形?证明你的结论.
②当AB与BC的比值为 时,四边形BEHC为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形使纸板做三棱柱盒子,每个盒子由3个长方形侧面和2个正三角形底面组成.硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)). A方法:剪6个侧面;
B方法:剪4个侧面和5个底面.
现有19张硬纸板,裁剪时x张用A方法,其余用B方法.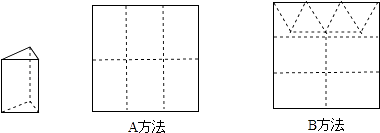
(1)分别求裁剪出的侧面和底面的个数(用x的代数式表示)
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com